|

Vamos agora analisar
o caso de difração de Fresnel e para isto vamos considerar
a Fig. 9.19, na qual as coordenadas da fonte e do observador são
dadas respectivamente por: S: (0,0,-h1) e P: (0,0,-h2).
Partindo da eq. (9.13) temos:
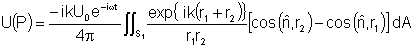
onde
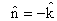 .
Fazendo as aproximações .
Fazendo as aproximações
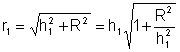
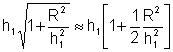 e
e
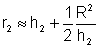 temos
temos
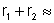
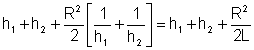 onde
onde
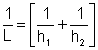 . .
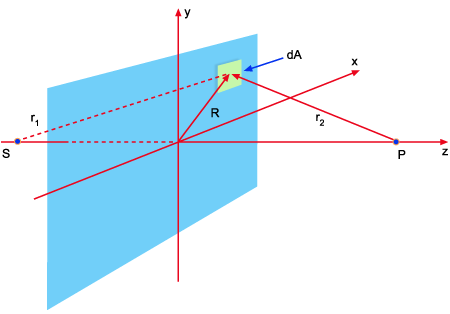
Fig. 9.19 - Geometria
para a difração de Fresnel.
Também tomamos
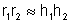 e assim obtemos:
e assim obtemos:
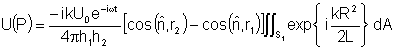
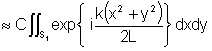
onde a constante defronte
a integral foi denominada C. Fazendo as substituições
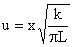 , ,
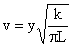 e
e
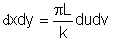 obtemos finalmente:
obtemos finalmente:
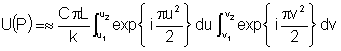
Façamos agora um breve parêntese para discutir as integrais
acima, as quais são chamadas integrais de Fresnel:
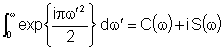
onde C(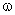 )
e S( )
e S(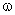 )
são dadas pela espiral de Cornu mostrada na Fig. 9.20. Quando: )
são dadas pela espiral de Cornu mostrada na Fig. 9.20. Quando:
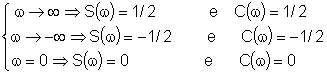
Logo,
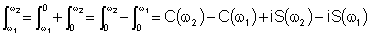
No caso que estamos estudando,
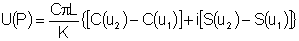
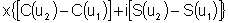
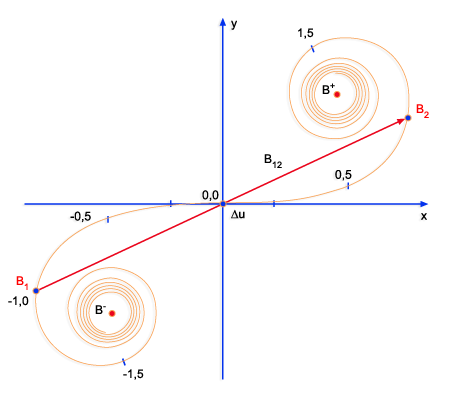
Fig. 9.20 - Espiral
de Cornu.
Sergio Carlos Zilio
|