| |
No caso de uma abertura
circular, vamos usar a variável y para integração,
similarmente ao que foi feito para a fenda estreita. Chamando de R
o raio da abertura, o elemento de área será tomado como
sendo uma faixa de comprimento
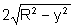e largura dy, como mostra a Fig. 9.14. Consideremos, dentro da aproximação
de Fraunhofer, que a onda incidente a abertura circular seja plana.
A amplitude da onda no ponto P é dada, de acordo com a eq.
(9.17), por:
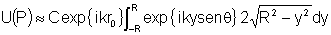
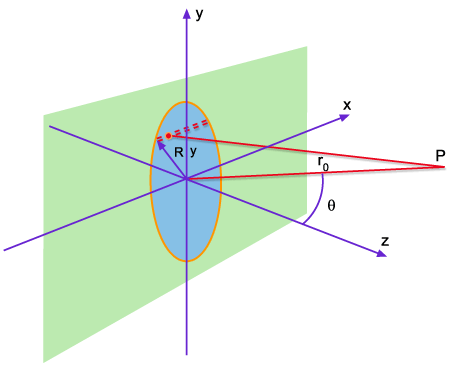
Fig. 9.14 - Ilustração
da geometria envolvida na difração por uma abertura
circular.
onde foi utilizado
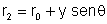e
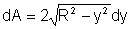. Introduzindo as grandezas u = y/R e
 ,
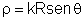a integral acima se torna:
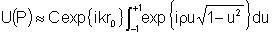
Esta é uma integral padrão (tabelada), cujo valor é
 ,
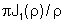onde
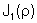 é
uma função especial chamada de função
de Bessel de primeira ordem. Desta forma, a intensidade do feixe difratado
se torna:
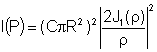
A dependência de Io em R4 nos indica uma
rápida redução (ou aumento) na intensidade de
luz com a diminuição (ou aumento) do raio da abertura
circular. Outro ponto importante a ser considerado é quanto
aos zeros da função
.
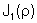Eles determinam os pontos de intensidade nula, os quais estão
localizados em círculos concêntricos em torno do ponto
 .
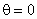As raízes da função
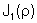ocorrem para os valores de
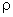iguais a 3.83, 7.02, 10.17, etc., como mostra a Fig. 9.15. Com eles
são obtidos os ângulos q que
correspondem à intensidade nula. Tais ângulos serão:
 ,
,
 .
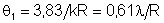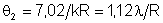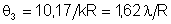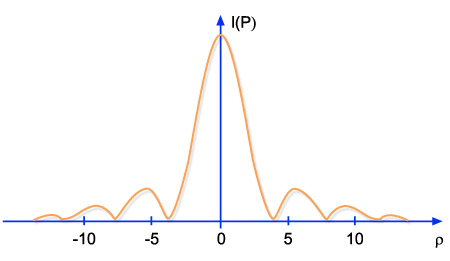
Fig. 9.15 - Padrão
de difração para uma abertura circular
Sergio Carlos Zilio
|
|
