No tratamento detalhado da difração é usual distinguir-se dois casos gerais conhecidos como difração de Fraunhofer e Fresnel. Qualitativamente falando, a difração de Fraunhofer ocorre quando as ondas incidente e difratada são planas. Este é o caso quando as distâncias r₁ e r₂ são tão grandes que a curvatura da frente de onda pode ser desprezada, como mostra a Fig. 9.8(a). Por outro lado, se a fonte e o ponto de observação estão suficientemente próximos da abertura temos então difração de Fresnel (Fig. 9.8(b)).

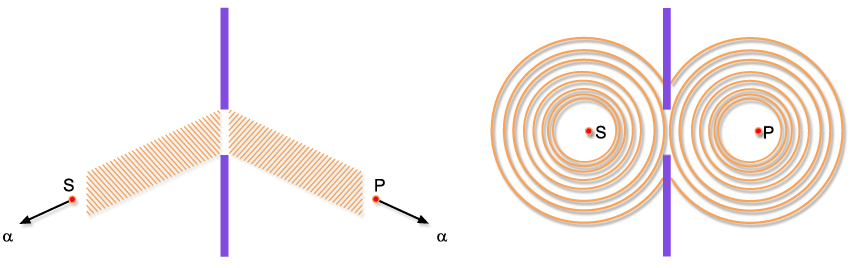
(a) Fraunhofer (b) Fresnel

Fig. 9.8 - Tipos de difração.

O arranjo experimental para se observar difração de Fraunhofer está mostrado na Fig. 9.9. Em particular, vamos analisar o caso da difração pela fenda estreita mostrada na Fig. 9.10. O campo elétrico no ponto P será dado por:

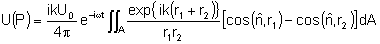
onde r₁ e r₂ são respectivamente as distâncias de S e P ao elemento de área dA. Levando-se em conta que os pontos S e P estão infinitamente afastados, de forma que r₁ e r₂ não variam muito ao fazer-se a integração sobre A, podemos escrever:

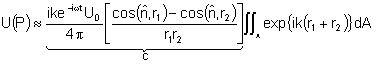
Fig. 9.9 - Arranjo para observar difração de Fraunhofer.

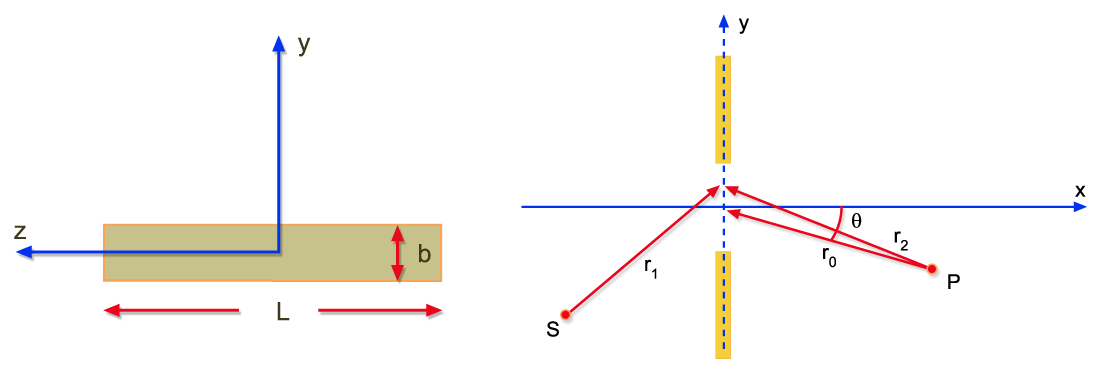
Fig. 9.10 - Fenda estreita (L >> b).

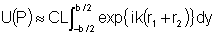
pois dA = Ldy. Uma segunda aproximação a ser feita é considerar r₁ constante sobre A. Além disto, 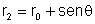, logo:

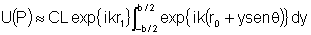
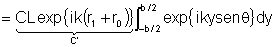
Esta última integral é fácil de ser calculada e nos leva a:

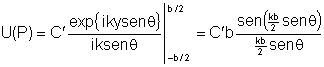
Fazendo 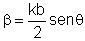, temos:

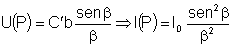
O padrão de difração I(P) está mostrado na Fig. 9.11. O máximo central ocorre para 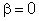( 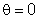) enquanto que os mínimos localizam-se em 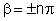, onde n é um inteiro. I(P) terá máximos relativos para 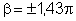, 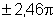etc. que são raízes de .

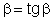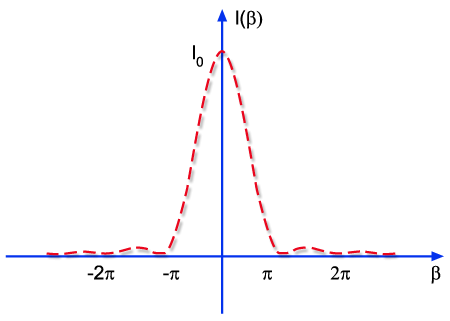
Fig. 9.11 - Padrão de difração para uma fenda estreita.

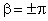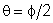Consideremos apenas a franja central para deduzir uma expressão para o ângulo no qual a luz se espalha. Para este fim vamos considerar a Fig. 9.12. Como os primeiros mínimos ocorrem para e , temos:

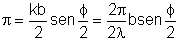
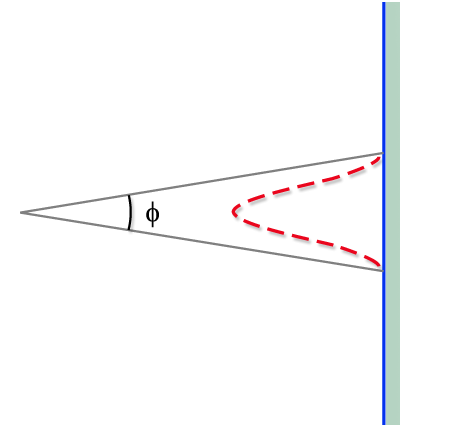
Fig. 9.12 - Ângulo de abertura da franja central.

Fazendo a aproximação de pequenos ângulos (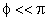), na qual sen 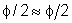, obtemos:

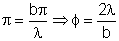
Esta expressão é bastante adequada para se observar a analogia entre a óptica ondulatória e a mecânica quântica. Nesta, um dos princípios fundamentais é o da incerteza (de Heisenberg) que estabelece para uma dimensão:

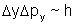
Para o problema de difração que estamos tratando, 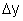pode ser identificado com a largura da fenda, b, enquanto que 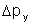é a incerteza no momentum do fóton, cujo valor é 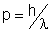, como demonstrado por de Broglie. Olhando para a Fig. 9.13, que é derivada da Fig. 9.13, vemos que a incerteza no momentum do fóton é 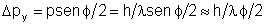. Assim,

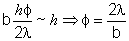
que reproduz a eq. 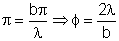, demonstrando a analogia entre a óptica ondulatória e a mecânica quântica.

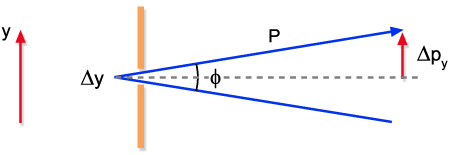
Fig. 9.13 - Ângulo de abertura da franja central.

No caso de uma fenda retangular, com os lados a e b da mesma ordem de grandeza, teremos:

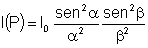
onde 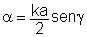. Deixaremos a demonstração desta expressão como exercício.

Sergio Carlos Zilio