|

Para mostrar como o grau
de coerência está relacionado com as características
da fonte, vamos considerar uma fonte quase monocromática com
a seguinte propriedade: o campo varia senoidalmente por um tempo
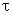 0,
chamado de tempo de coerência, e então muda de fase abruptamente.
Esta sequência se repete indefinidamente e a mudança
de fase que ocorre a cada 0,
chamado de tempo de coerência, e então muda de fase abruptamente.
Esta sequência se repete indefinidamente e a mudança
de fase que ocorre a cada
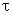 0está
aleatóriamente distribuida entre 0 e 0está
aleatóriamente distribuida entre 0 e
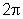 ,
como mostra a Fig. 8.2. ,
como mostra a Fig. 8.2.
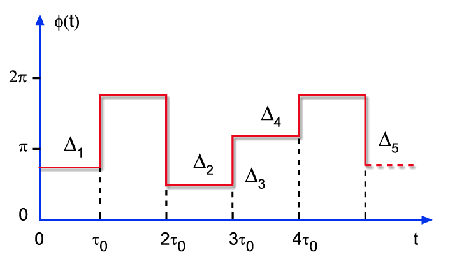
Fig. 8.2 - Variação aleatória da fase
a cada intervalo de tempo ?0
O campo elétrico pode ser expresso como:
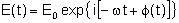
Supondo novamente que
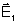 e
e
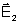 são paralelos e que possuem a mesma amplitude, temos:
são paralelos e que possuem a mesma amplitude, temos:
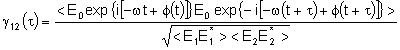
e portanto,
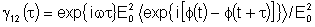
Escrevendo a média temporal de forma explícita obtemos:
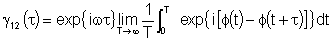
Para resolver esta integral devemos considerar dois casos:
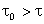 e
e
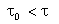 ,
que serão analisados a seguir. ,
que serão analisados a seguir.
Caso a)
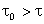
A Fig. 8.3 mostra como
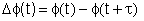 varia com o tempo. Para
varia com o tempo. Para
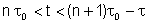 temos
temos
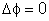 e para
e para
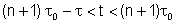 ,
temos ,
temos
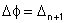 .
Logo, realizando explicitamente a integral temos: .
Logo, realizando explicitamente a integral temos:
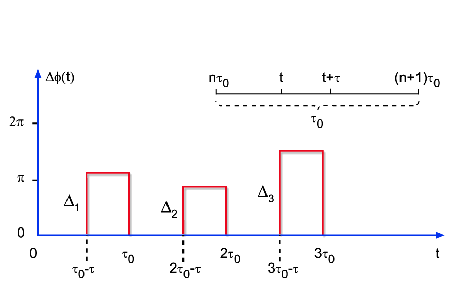
Fig. 8.3 - Variação
de
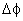 com o tempo.
com o tempo.
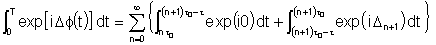
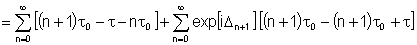
A segunda somatória é nula pois as variações
de fase são aleatórias e quando somamos
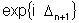 ,
os vários termos se cancelam. Assim sendo, substituímos
a eq. ,
os vários termos se cancelam. Assim sendo, substituímos
a eq.
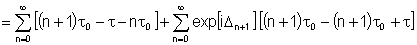 em
em
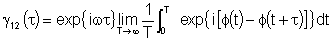 e obtemos:
e obtemos:
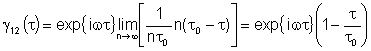
Caso b)
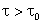
Agora,
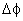 será
sempre diferente de zero pois em t e t + será
sempre diferente de zero pois em t e t +
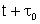 as fases são diferentes. Assim, temos um termo
as fases são diferentes. Assim, temos um termo
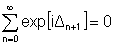 e não teremos o termo não nulo em que
e não teremos o termo não nulo em que
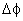 = 0. Assim, para
= 0. Assim, para
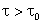 teremos sempre
teremos sempre
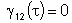 . .
Para utilizarmos a eq.
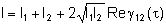 ,
devemos tomar a parte real de ,
devemos tomar a parte real de
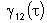 ,
dada por: ,
dada por:
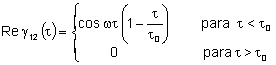
Com este resultado, podemos fazer o gráfico de
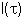 ,
mostrado na Fig. 8.4. Se I1 = I2 = I0,
temos ,
mostrado na Fig. 8.4. Se I1 = I2 = I0,
temos
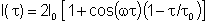 para
para
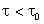 e 2I0 para
e 2I0 para
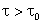 . .
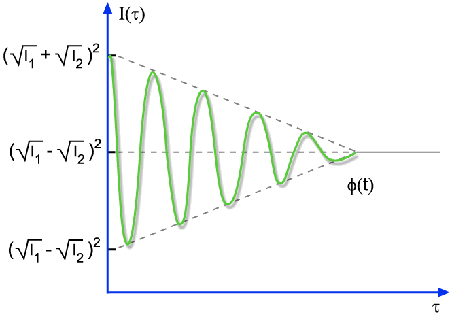
Fig. 8.4 - Interferência
entre dois feixes parcialmente coerentes.
Podemos ainda chamar
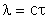 como diferença de caminhos ópticos (supondo que n =
1) e
como diferença de caminhos ópticos (supondo que n =
1) e
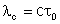 como comprimento de coerência. Se quisermos ter interferência
estacionária a desigualdade
como comprimento de coerência. Se quisermos ter interferência
estacionária a desigualdade
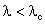 deve ser satisfeita. A seguir, vamos ver alguns exemplos numéricos
para diferentes tipos de luz e para isto vamos usar a expressão
deve ser satisfeita. A seguir, vamos ver alguns exemplos numéricos
para diferentes tipos de luz e para isto vamos usar a expressão
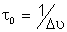 ,
onde ,
onde
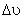 é a largura de linha, que será demonstrada na seção
seguinte. Consideremos então as seguintes fontes emissoras
de luz:
é a largura de linha, que será demonstrada na seção
seguinte. Consideremos então as seguintes fontes emissoras
de luz:
i) Lâmpada espectral: temos tipicamente
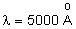 e
e
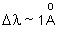 .
O comprimento de coerência é .
O comprimento de coerência é
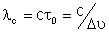 .
Mas .
Mas
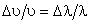 ou
ou
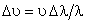 que nos leva a
que nos leva a
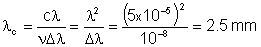
ii) Luz branca: agora temos
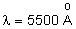 e
e
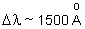 ,
que resulta em ,
que resulta em
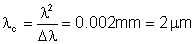
iii) Radiação coerente (laser): um valor típico
para
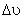 é de 104 Hz . Logo,
é de 104 Hz . Logo,
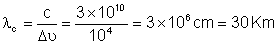
Sergio Carlos Zilio
|