Um outro ponto interessante a ser tratado neste capítulo é como o fato de um trem de ondas não ser temporalmente infinito altera sua composição espectral. Considere o campo elétrico E(t) num certo ponto do espaço. Esta função está relacionada com a transformada de Fourier da função g(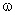), que dá a composição espectral do campo através da transformação:

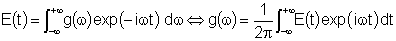
Tomemos um trem de ondas temporalmente finito, como o mostrado na Fig. 8.5. Ele pode ser expresso como:

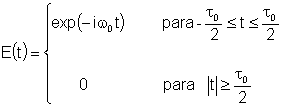
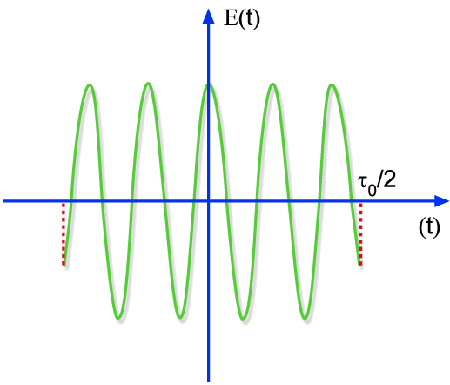
Fig.8.5 - trem de ondas finito

Desta forma, podemos encontrar g(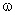) dado pela eq. 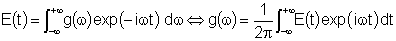como:

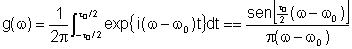
que podemos re-escrever como:

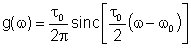
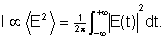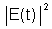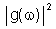A intensidade do feixe é Entretanto, através do teorema de Parceval podemos relacionar e como:

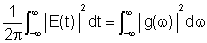
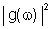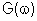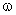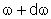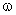Vamos chamar de , que é a função de distribuição espectral, ou seja, a energia do trem compreendida entre e . As duas funções g () e G (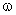) estão esboçadas na Fig. 8.6. G(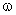 ) é dado por: 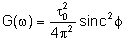, onde 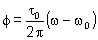. Notando que 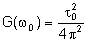, podemos encontrar as frequências que dão a meia largura do pico central através de:

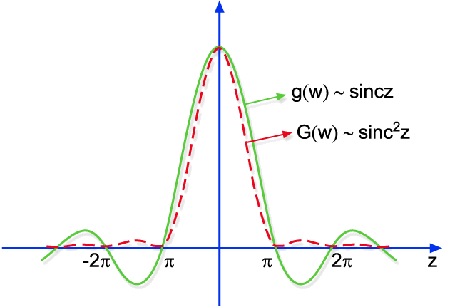
Fig. 8.6 - Composição espectral do campo elétrico, g(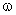) e função de distribuição espectral, G().

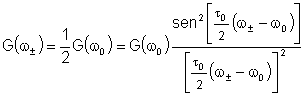
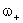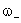Esta igualdade pode ser resolvida para nos dar os valores de e com os quais se calcula a meia largura da distribuição espectral:

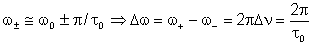
Logo, a largura da linha espectral está relacionada com o tempo de coerência através de:

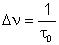
expressão esta que já foi utilizada para o cálculo dos comprimentos de coerência de diferentes fontes de luz.

Sergio Carlos Zilio