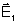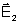No capítulo anterior deduzimos fórmulas para a interferência de ondas eletromagnéticas supondo serem elas monocromáticas, coerentes e de amplitudes constantes. Em casos reais, a amplitude e a fase variam com o tempo de maneira aleatória, produzindo assim, intensidades de luz que flutuam rapidamente. No caso da superposição dos campos e , a intensidade será, a menos de constante multiplicativa, dada por:

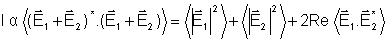
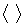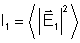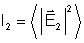onde significa média temporal, e . No que segue, vamos supor qu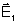e e 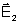são paralelos. A Fig. 8.1 mostra um caso típico de interferência. Supondo que os feixes 1 e 2 deixam fonte S em t = 0, eles chegarão ao ponto de observação P após decorridos os tempos t e 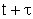, respectivamente, posto que caminham distâncias diferentes. Logo, E₁ = E₁(t) e .

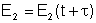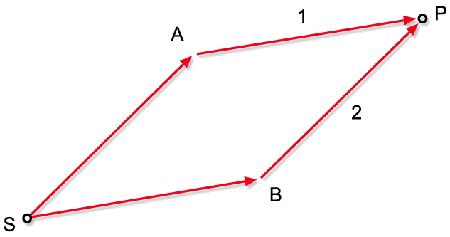
Fig. 8.1 - Interferência de dois campos E₁ e E₂.

Na expressão para a intensidade temos um termo “cruzado” em 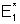e 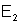. Vamos definir uma função de correlação ou coerência mútua como:

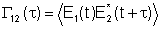
e a função de correlação normalizada:

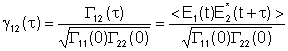
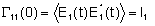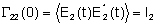onde e 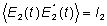. Assim, com base nas equações

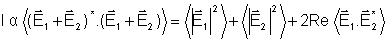  e 

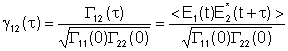
podemos escrever:

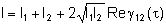
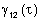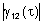A função é geralmente uma função periódica de t. Portanto, teremos um padrão de interferência se , chamado de grau de coerência, tiver um valor diferente de 0. Em termos de 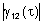temos os seguintes tipos de coerência:

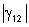= 1 Coerência completa
0 < 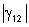< 1 Coerência parcial
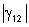= 0 Incoerência completa

No capítulo anterior definimos visibilidade das franjas como:

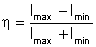
Como a função 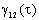pode ser positiva ou negativa, temos:

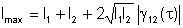
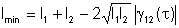
Logo, em termos de 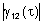a visibilidade é dada por:

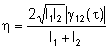
e no caso particular em que I₁ = I₂, 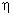assume uma expressão simples:

Desta forma, para intensidades de mesmo valor, a visibilidade das franjas nos indica o grau de coerência da luz.

Sergio Carlos Zilio