No nosso estudo de interferência nos concentramos até agora no problema de interferência entre apenas dois feixes. Queremos agora tratar o problema de interferência entre múltiplos feixes. Uma maneira de se produzir um grande número de feixes mutuamente coerentes é por reflexão múltipla entre duas superfícies planas e paralelas parcialmente refletores, como por exemplo, a placa de vidro mostrada na Fig. 7.9.

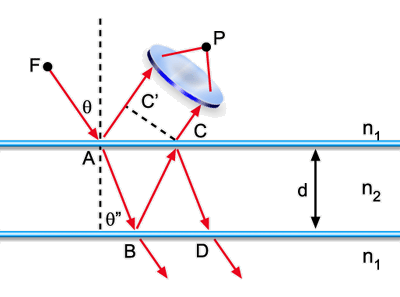
Fig. 7.9 - Interferência por múltiplas reflexões.

Vamos inicialmente considerar apenas os raios (1) e (2) atingindo o ponto P. Posteriormente tomaremos um número maior de raios. Tomando a origem da propagação no ponto A, a situação do campo elétrico será:

Em A:		Incidente: E0 exp{-iw t} Refletido: rE0 exp{-iw t} Transmitido: tE0 exp{-iw t}	(7.22a)
			(7.22b)
			(7.22c)

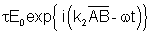
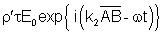
Em B:		Incidente: Refletido: Transmitido:	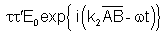(7.23a)
			(7.23b)
			(7.23c)

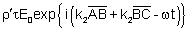
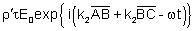
Em C:		Incidente: Refletido: Transmitido:	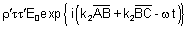(7.24a)
			(7.24b)
			(7.24c)

A frente de onda é constituída pelos campos em C e C', dados por:

	(7.25a)
	(7.25b)

onde 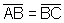. Por outro lado, vemos qu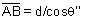e e 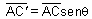implicando que 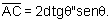Definimos:

	(7.26a)
	(7.26b)

Podemos ainda obter através das equações de Fresnel que r = -r' e tt'=1-r². Desta forma o campo elétrico total na frente de onda será:

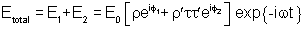A

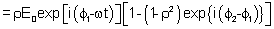
(7.27)

de forma que a intensidade será proporcional a:

(7.28)

Se tivermos trabalhando com vidros teremos r ~ 0,2 ® r² = 0,04 ® (1-r²)=0,96 ~ 1. Então:

(7.29)

A diferença de fases é:

(7.30)

Usando a lei de Snell, 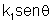= 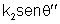, temos:

(7.31)

As condições de máximo e mínimo de interferência são dadas respectivamente por:

(7.32a)

(7.32b)

Sergio Carlos Zilio