|

Na
discussão do princípio da superposição
feita na seção anterior, foram utilizados apenas dois
feixes para simplificar a análise, mas o princípio é
válido para um número arbitrário deles, conforme
abordaremos nas seções posteriores. Em dispositivos
interferométricos que utilizam dois feixes costuma-se dividir
a frente de onda e isto pode ser feito de várias maneiras,
como veremos a seguir.

Um
experimento clássico que demonstra a interferência da
luz foi feito por Thomas Young, em 1802. Considere o arranjo experimental
mostrado na Fig. 7.4. Luz proveniente de uma fonte F passa por um
pequeno orifício S e incide sobre duas fendas paralelas estreitas
S1 e S2 separadas por uma distância h.
Um anteparo colocado após as fendas mostrará listas
claras e escuras, definindo assim o padrão de interferência
que estamos interessados em encontrar. Note que o orifício
S é de fundamental importância pois é ele que
fornece a coerência espacial necessária entre a radiação
vinda das duas fendas.
Como vimos anteriormente na eq. (7.11),
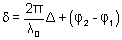 , onde , onde
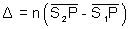 é a diferença de caminhos ópticos. Usandi
o teorema de Pitágoras temos: é a diferença de caminhos ópticos. Usandi
o teorema de Pitágoras temos:
que
são expressões válidas apenas quando h <<
D. Desta forma,
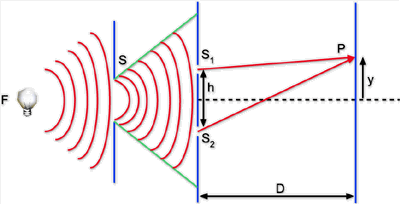
Fig. 7.4 - Experimento de Young para a observação de
interferência.
Vamos agora supor que n=1 (vácuo) e f1
= f2 (feixes coerentes). Disto
resulta que:
Para
se obter intensidade máxima devemos ter:
e
intensidade mínima quando:
A
Fig. 7.5 mostra o padrão de interferência que se observa
no anteparo. A distância entre duas franjas consecutivas (dois
máximos consecutivos), chamada interfranja é
dada por:

Fig. 7.5 - Padrão de interferência obtido com a fenda dupla.
Maneiras
alternativas de se demonstrar interferência por divisão
da frente de ondas são vistas na Fig. 7.6. Dentre elas se incluem
também os interferômetros de Michelson e de Mach-Zehnder,
que devido a sua importância serão tratados separadamente.

O
interferômetro de dois feixes mais conhecido foi desenvolvido
por Michelson em 1880. O desenho básico está mostrado
na Fig. 7.7. A radiação proveniente de uma fonte F é
colimada e dividida por um divisor de feixes DF. Os feixes divididos
são refletidos pelos espelhos E1 e E2
e voltam para o divisor de feixes. O padrão de interferência
é observado em P, ao se variar a posição de um
dos espelhos.
Supondo ser a fonte monocromática e o interferômetro
estar no vácuo (n = 1), a diferença de caminhos ópticos
é dada por D= x1 - x2
e portanto a diferença de fase é:
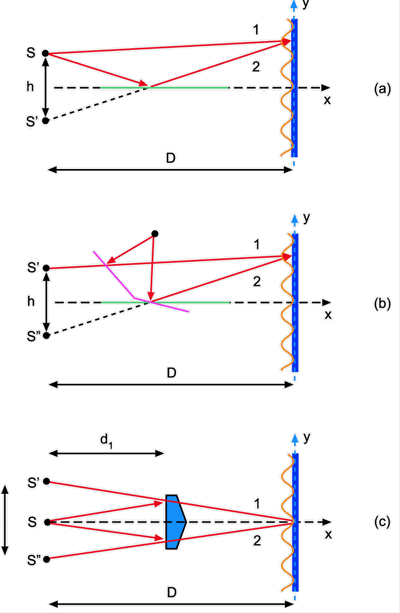
Fig. 7.6 - Alguns dispositivos que produzem interferência por
divisão de frente de onda:
(a)
espelho simples de Lloyd, (b) espelho duplo de Fresnel e (c) biprisma
de Fresnel.
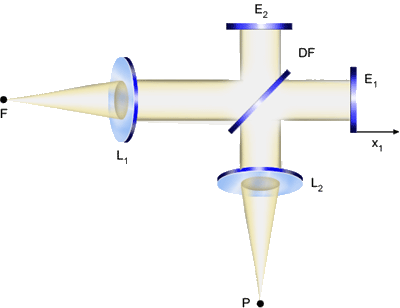
Fig. 7.7 - Interferômetro
de Michelson.
onde
x1 e x2 são respectivamente as distâncias
percorridas pelos feixes 1 e 2. A intensidade observada em P é:
Como
os feixes 1 e 2 são refletidos e transmitidos de maneira igual
pelo divisor D, temos I1 = I2 = I0.
Desta forma,
Observando
que I(0) = 4I0, podemos re-escrever a eq. (7.19) como:
ou,
alternativamente:
É interessante notar que P(D ) é
a transformada de Fourier do espectro da fonte, isto é, de
uma função
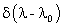 .
Este instrumento é usado para fazer espectroscopia com transformada
de Fourier da seguinte maneira: mede-se I(D
) variando-se a posição de um dos espelhos, subtrai-se .
Este instrumento é usado para fazer espectroscopia com transformada
de Fourier da seguinte maneira: mede-se I(D
) variando-se a posição de um dos espelhos, subtrai-se
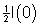 para a obtenção de P(D )
e em seguida faz-se a transformada de Fourier que nos dá o
espectro B(l ) da fonte. Voltaremos a falar deste instrumento no Cap.
8.
para a obtenção de P(D )
e em seguida faz-se a transformada de Fourier que nos dá o
espectro B(l ) da fonte. Voltaremos a falar deste instrumento no Cap.
8.

Um
outro interferômetro de dois feixes importante é o interferômetro
de Mach-Zehnder. O desenho básico está mostrado na Fig.
7.8 e o princípio de funcionamento é similar ao de Michelson.
A radiação proveniente de uma fonte F é colimada
e dividida por um divisor de feixes DF1. Os feixes divididos
são refletidos pelos espelhos E1 e E2
e vão para um outro divisor de feixes DF2. O padrão
de interferência é observado na saida 1 ou na saida 2,
ao se variar a posição de um dos espelhos.
A característica principal deste instrumento é que variando-se
a diferença de caminhos ópticos é possível
fazer com que a luz comute entre uma e outra saida. Isto tem importância
em comunicações ópticas porque possibilita alterar
a direção de tráfego do sinal. Já no caso
do interferômetro de Michelson, a luz ou vai para o observador,
ou retorna para a fonte.
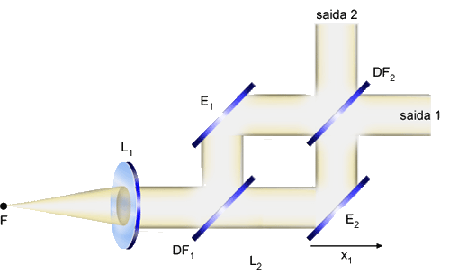
Fig. 7.8 - Interferômetro de Mach-Zehnder.
Sergio Carlos Zilio
|