|

Interferência
é o fenômeno que tem como origem a adição
vetorial dos campos eletro-magnéticos (princípio da
superposição). Ao se calcular a intensidade do campo
resultante, através da eq. (4.41), veremos que esta pode ser
maior ou menor que a soma das intensidades dos campos que se superpuseram.
Em geral, estes são oriundos da mesma fonte e percorrem caminhos
ópticos distintos, de forma que haverá uma diferença
de fase entre eles. A Fig. 7.1 mostra um exemplo de como o processo
de interferência pode ser obtido. Para efeitos práticos,
é como se os raios 1 e 2 fossem provenientes de duas fontes
virtuais, F' e F''. Vários outros casos serão descritos
posteriormente. Veremos no Cap. 8 que se a fonte for coerente teremos
interferência estacionária, ao passo que se a
fonte for incoerente teremos interferência não
estacionária.
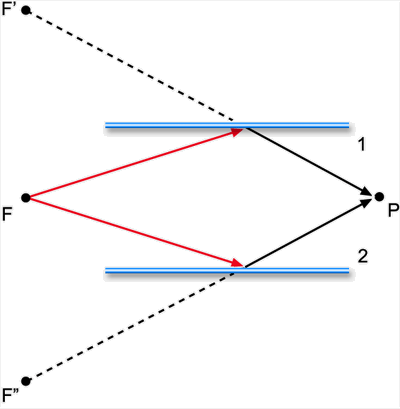
Fig. 7.1 - Diagrama esquemático mostrando a obtenção
de interferência.
Para
entender melhor o princípio da superposição,
vamos considerar duas fontes pontuais F1 e F2
emitindo ondas esféricas, monocromáticas e coerentes
num meio não polarizável (vácuo) conforme está
mostrado na Fig. 7.2. No ponto P temos:
que
são os campos produzidos pelas fontes F1 e F2,
respectivamente.
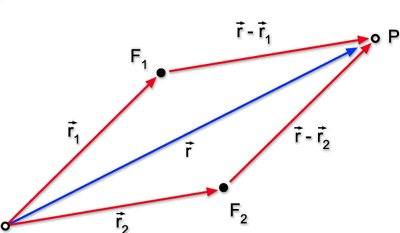
Fig. 7.2 - Arranjo para a observação de interferência
de duas
fontes pontuais monocromáticas.
O
campo resultante
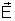 vem da superposição de
vem da superposição de
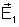 e
e
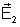 ,
isto é, da adição vetorial ,
isto é, da adição vetorial
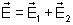 . A intensidade é proporcional a . A intensidade é proporcional a
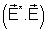 ,
logo:- ,
logo:-
Os
dois últimos termos são aqueles responsáveis
pela interferência, como veremos a seguir. Podemos escrever
estes termos como:
Supondo
que
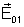 e
e
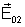 são paralelos e definindo:
são paralelos e definindo:
temos:
ou
alternativamente,
onde
o último termo, oriundo da mistura de
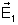 e
e
 varia com a
diferença de fase entre os campos e dá origem ao fenômeno
chamado interferência. Para a obtenção da eq.
(7.6) tomamos varia com a
diferença de fase entre os campos e dá origem ao fenômeno
chamado interferência. Para a obtenção da eq.
(7.6) tomamos
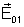 e
e
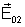 paralelos. Se isto não ocorrer, o termo de interferência
deverá ser multiplicado por cos
paralelos. Se isto não ocorrer, o termo de interferência
deverá ser multiplicado por cos
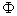 ,
onde ,
onde
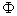 é o ângulo entre
é o ângulo entre
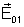 e
e
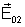 .
Voltando à análise da eq. (7.6), podemos ver que a intensidade
máxima é: .
Voltando à análise da eq. (7.6), podemos ver que a intensidade
máxima é:
que
é maior que a soma
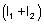 . Isto acontece quando o co-seno vale 1, ou seja, quando d
= 2np (interferência construtiva). Por outro lado, a intensidade
mínima é dada por: . Isto acontece quando o co-seno vale 1, ou seja, quando d
= 2np (interferência construtiva). Por outro lado, a intensidade
mínima é dada por:
que
é menor que
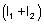 . Isto acontece para cos d = 1, ou
seja, quando d = (2n+1)p (interferência destrutiva). A Fig. 7.3 mostra como
a intensidade varia com d. . Isto acontece para cos d = 1, ou
seja, quando d = (2n+1)p (interferência destrutiva). A Fig. 7.3 mostra como
a intensidade varia com d.
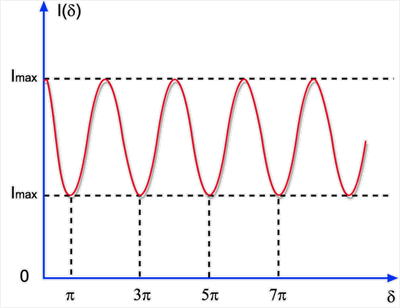
Fig. 7.3 - Intensidade
dos campos superpostos com função da diferença
da fase.
No
caso em que I1 = I2 = I0 temos Imax
= 4I0 e Imin = 0. Costuma-se definir a visibilidade
das franjas (visibilidade de Michelson) como:
No caso particular em que f1
= f2 temos
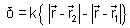 , de forma que se considerarmos os máximos, veremos que
eles satisfazem: , de forma que se considerarmos os máximos, veremos que
eles satisfazem:
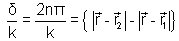 = const = const |
(7.9) |
que
é um hiperbolóide de revolução. d pode ser colocado em termos da diferença de caminhos
óticos, que neste caso é dada por:
Logo:
Geralmente
f1 = f1(t)
e f2 = f2(t),
isto é, as fases mudam com o tempo. Chamando t0 de tempo de coerência, que é
um tempo característico ligado à mudança de fase,
e T de tempo de observação, quando t0<<
T temos interferência não estacionária. Voltaremos
a este tópico no Cap. 8.
Sergio Carlos Zilio
|