|

Na
análise que fizemos até agora dos fenômenos envolvendo
a fase, as partes espacial e temporal eram independentes, do tipo
f(z,t)= kz - wt. Assim, a identificação
da frequência da onda, associada à evolução
temporal da fase, era imediata. Entretanto, podem ocorrer situações
onde o índice de refração, e consequentemente
o vetor de propagação, depende do tempo. Desta forma,
a fase da onda torna-se f(z,t)= k(t)z - wt, e as partes espacial
e temporal ficam misturadas pelo primeiro termo. Como a frequência
encontra-se associada à evolução temporal da
fase da onda eletromagnética, podemos definir:
como sendo a frequência generalizada da onda. Com este conceito
podemos analisar alguns efeitos responsáveis pelo surgimento
de novas componentes de frequência. Começaremos com o
efeito eletro-óptico que pode modificar a frequência
da onda, ou introduzir novas componentes de frequência, como
veremos a seguir.
Existem cristais anisotrópicos não lineares (KDP, LiNbO3,
LiTaO3, etc.) cujos índices de refração se modificam
com a aplicação de um campo elétrico externo.
Estes cristais são denominados eletro-ópticos. Consideremos
uma onda propagando-se pelo cristal ao longo do eixo óptico
z, com polarização na direção do eixo
x, conforme mostra a Fig. 5.9. Um campo elétrico variável
no tempo é aplicado, também na direção
do eixo x. O índice de refração é dado
por: n(t) = n0
+ aV(t), onde V(t) é a voltagem
aplicada, é a resposta do cristal ao campo externo e n0
é o índice de refração na ausência
de campo. Esta variação do índice de refração
produz uma alteração na fase da onda, que passa a ser:
| f(t) = k0n0L- w0t + k0aLV(t) |
|
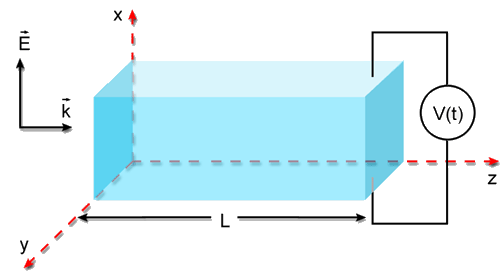
Fig. 5.9 - Propagação de uma onda eletromagnética
ao longo de um cristal eletro-óptico.
onde
L é o comprimento do cristal, 0 é a frequência
da luz incidente e k0 é o vetor de onda no vácuo. Vamos
em seguida considerar dois tipos de voltagens aplicadas sobre o cristal,
que são os casos de maior interesse prático.

Nesta
situação, V(t) = bt, e a fase de onda fica:
| f(t) = k0n0L- w0t + k0aLbt |
|
de
forma que obtemos a frequência generalizada como:
isto
é, o cristal eletro-óptico faz variar um pouco a frequência
da luz, como mostrado na Fig. 5.10.

Neste
caso, temos V(t) = Asen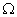 t,
onde t,
onde
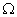 é uma frequência gerada por uma fonte de rádio-frequência
(em geral da ordem de 100 MHz), de forma que:
é uma frequência gerada por uma fonte de rádio-frequência
(em geral da ordem de 100 MHz), de forma que:
f(t) = k0n0L- w0t + k0aLAsen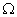 t t |
|
que dá origem à uma frequência:
Fig.
5.10 - Alteração da frequência da luz ao passar
por um cristal eletro-óptico com voltagem do tipo rampa.
que
é modulada pelo termo cos t.
Para entendermos como esta modulação altera o espectro
de frequência da luz, vamos analisar o que acontece com a onda
plana neste caso. t.
Para entendermos como esta modulação altera o espectro
de frequência da luz, vamos analisar o que acontece com a onda
plana neste caso.
E = E0
exp{i (k0n0L- w0t + k0aLAsen t)} t)} |
|
O
termo exp{i Msen t},
com M = k0LA, pode ser expandido
numa série de funções de Bessel de acordo com: t},
com M = k0LA, pode ser expandido
numa série de funções de Bessel de acordo com:
de
forma que o campo elétrico é dado por:
de onde vemos a criação de vários picos laterais
à frequência fundamental 0. Lembrando-se que J-n (M) = (-1)n Jn(M), temos um novo
espectro de frequência da luz, que é mostrado na Fig.
5.11. Este tipo de modulação tem suas principas aplicações
na geração de novas frequências para espectroscopia
com laser e no "mode-locking" de lasers.
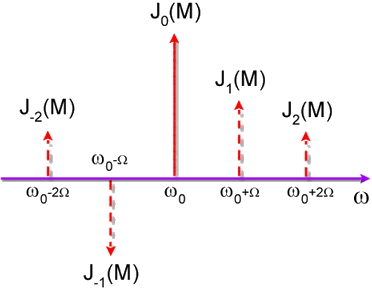
Fig. 5.11 - Geração de picos laterais (sidebands) através
de modulação eletro-óptica.
Sergio Carlos Zilio
|