|

O
efeito Doppler e a aberração da luz das estrelas, descoberta
por Bradley em 1725, podem ser explicados em termos da relatividade
restrita, introduzida em 1905 por Albert Einstein. Vamos inicialmente
rever alguns de seus conceitos básicos:

a)
As leis físicas são invariantes em forma para diferentes
referenciais inerciais (referenciais não acelerados).
b)
A velocidade da luz é a mesma para todos os observadores inerciais.

Considere dois sistemas de coordenadas cartesianas O e O', sendo que
O' se move com velocidade
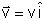 ,
como mostra a Fig. 5.7. No instante t =
0 as duas origens coincidem. As transformações de Lorentz
relacionam (x,y,z,t) do referencial O com (x',y',z',t') do referencial
O', de acordo com: ,
como mostra a Fig. 5.7. No instante t =
0 as duas origens coincidem. As transformações de Lorentz
relacionam (x,y,z,t) do referencial O com (x',y',z',t') do referencial
O', de acordo com:
| x = g(x'+vt') |
x' = g(x-vt) |
| y = y' |
y' = y |
| z = z' |
z' = z |
| t= g(t'+vx'/c2) |
t' = g(t-vx/c2) |
|
|
Onde
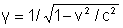 . .

Como vimos em (ii), as coordenadas espaciais e temporal estão
intimamente ligadas, por isso é conveniente se trabalhar com
vetores de quatro componentes (quadrivetor). Exemplos de quadrivetores
são os de posição, vetor de onda e momentum,
respectivamente mostrados abaixo:
Fig. 5.7 - Referenciais com movimento relativo.
O
produto escalar de dois quadrivetores é feito como normalmente
se multiplicam matrizes. Como exemplo, tomemos o produto dos dois
primeiros quadrivetores mostrados acima:
f = kxx + kyy + kzz
- wt= 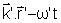 |
|
que
é exatamente a fase da onda plana. Como o produto escalar de
quadrivetores é invariante quando se muda de um referencial
inercial para outro, a fase da onda plana é a mesma quando
vista por observadores em O e O'.

Considere
uma onda plana propagando-se na direção do eixo x (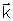 = k î). A fase vista pelo observador
em O será f = kx - wt e em O' será
f' =
= k î). A fase vista pelo observador
em O será f = kx - wt e em O' será
f' =
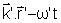 = kx'x'+ ky'y'+ kz'z' - w't', isto é, estamos supondo que em O' a onda
se propaga numa direção arbitrária. Como f
=f' temos:
= kx'x'+ ky'y'+ kz'z' - w't', isto é, estamos supondo que em O' a onda
se propaga numa direção arbitrária. Como f
=f' temos:
| kx - w = k'xx'+ k'yy'+
k'zz' - w't' |
|
Usando
as transformações dadas pela eq. (5.23), obtemos:
Igualando
os coeficientes de cada coordenada temos as seguintes relações:
ky' = kz'
= 0
kx' = g(k-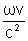 )
)
w' = g(w-kv)
|
|
Mas
como k = w/c então
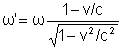 ,
e consequentemente, ,
e consequentemente,
que
é a fórmula do efeito Doppler longitudinal obtida pela
relatividade restrita. Para recuperarmos a fórmula clássica
devemos expandir este resultado para v<<c.

Considere agora a onda plana se propagando na direção
do eixo y (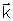 = k
= k
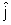 ),
sendo portanto perpendicular a ),
sendo portanto perpendicular a
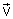 . As fases vistas em O e O' são respectivamente: f
= ky - wt e f' = . As fases vistas em O e O' são respectivamente: f
= ky - wt e f' =
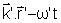 = kx'x'+ ky'y'+ kz'z'
- w't'. Igualando estes dois escalares chegamos a: = kx'x'+ ky'y'+ kz'z'
- w't'. Igualando estes dois escalares chegamos a:
Novamente,
usando as transformações dadas pela eq. (5.23), obtemos:
de
onde tiramos as seguintes relações:
kz' = 0
kx' = -
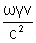
kx' = k = w/c
w' = g(w-kv)
|
(5.31a)
(5.31b)
(5.31c)
(5.31d)
|
sendo
que esta última expressão nos dá a fórmula
do efeito Doppler transversal, que não possui análogo
clássico.

De acordo com as eq. (5.31), vemos que a direção de
propagação da onda plana no referencial O' não
é na direção de y', mas forma com este um ângulo
dado por:
Este
fenômeno de mudança de direção é
conhecido como aberração da luz das estrelas. Devido
ao fato de que um observador na Terra tem uma velocidade finita ele
verá a posição da estrela diferente da posição
real que ela ocupa, devido ao problema de aberração
citado acima. A Fig. 5.8 mostra este efeito.
Fig. 5.8 - Aberração da luz proveniente das estrelas.
Sergio Carlos Zilio
|