O funcionamento de lâmpadas de descarga e lasers a gás baseia-se no fato de que os átomos são excitados pela descarga elétrica e ao voltarem para o estado fundamental emitem luz de frequência n₀ = E/h, onde E é a diferença de energia entre os estados fundamental e excitado, e h é a constante de Planck. Note que aqui estamos denominando a frequência de , enquanto que na seção anterior a mesma era f. Entretanto, devido ao fato das moléculas do gás possuirem movimento browniano, a linha n₀ adquire uma largura Dn que queremos calcular.

Vamos considerar um gás com n moléculas/cm³, mantido à temperatura T num tubo de Geisler. Após a descarga elétrica observa-se a luz emitida na direção do eixo x com um espectrofotômetro, dando-se particular atenção à raia de frequência em torno de n₀. O número de moléculas/cm³ com componente x de velocidade compreendida entre v_x e v_x + dv_xé dada por:

(5.18)

Admitamos que a intensidade total Idn emitida com frequência compreendida no intervalo n e n + d é proporcional a dn. Assim temos:

(5.19)

Entretanto, v_x e dv_x podem ser tirados da fórmula do efeito Doppler na qual a fonte está em movimento e o observador em repouso, eq. (5.15). Expandindo o denominador para v_x/c << 1 chegamos a:

(5.20)

Logo, dv_x = (c/n₀)dn . Desta forma, cancelando d na expressão para I e usando a eq. (5.20) obtemos :

(5.21)

que é a expressão da gaussiana mostrada na Fig. 5.6.

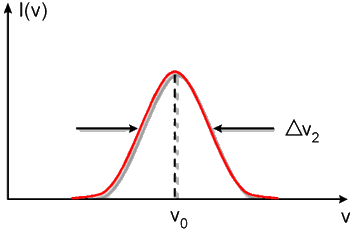
Fig. 5.6 - Alargamento espectral devido ao efeito Doppler.

Se as moléculas do gás estivessem em repouso, o espectro de frequências observado seria a função d(n - n₀). Entretanto, como elas se movem, o efeito Doppler faz com que haja um alargamento desta linha. É fácil mostrar que a largura da linha, Dn_D, é dada por:

(5.22)

Sergio Carlos Zilio