|

Na
seção anterior aprendemos a calcular a velocidade da
onda eletromagnética. Vamos agora dedicar o restante do capítulo
à analise de fatores que determinam sua frequência, começando
pelo famoso efeito Doppler.
Consideremos uma fonte S emitindo radiação eletromagnética
de frequência f, num meio com índice de refração
unitário, e um observador O. Temos quatro casos a tratar:
a) O observador se aproxima da fonte com velocidade v0.
Neste caso, o número de ondas que ele encontra num tempo t é:
onde
v0t é a distância
que ele percorre num tempo t. Como c =
lf, temos f' = f (1+v0/c).
Desta forma, o observador nota que a frequência da luz aumenta
por um fator (1+v0/c) devido ao fato dele estar se aproximando da fonte.
b) O observador se afasta da fonte com velocidade v0.
Este caso é similar ao anterior, apenas deve-se inverter o
sinal de v0:
c)
A fonte se aproxima do observador com velocidade vs.
Olhando para a Fig. 5.4 vemos que durante um certo tempo t, a frente de onda percorre uma distância
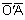 = tc , enquanto que a fonte anda
= tc , enquanto que a fonte anda
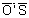 = vst ,. A distância
= vst ,. A distância
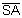 é dada por
é dada por
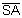 = tc - vst =
(c-vs)t . Assim, o comprimento de onda na região
= tc - vst =
(c-vs)t . Assim, o comprimento de onda na região
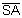 é dado por: l =
é dado por: l =
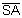 /número
de ondas = /número
de ondas =
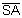 /ft e portanto, /ft e portanto,

Fig. 5.4 - Demonstração do efeito Doppler no caso
em que a fonte se aproxima do observador.
A
frequência f' observada por O será então dada
por:
d)
A fonte se afasta do observador com velocidade vs,
de forma que basta inverter o sinal no denominador:
Estes
quatro casos podem ser resumidos em apenas uma expressão matemática:
onde
o sinal das velocidades será positivo se elas estiverem no
sentido do observador para a fonte. No caso de estarmos tratando com
luz visível, o efeito chama-se Doppler-Fizeau. Exemplo disto
são as aplicações astronômicas:
(i) Estrelas duplas: são duas estrelas bastante próximas
girando em torno do centro de massa do sistema, não separáveis
através de telescópio. Porém, ao analisar-se
o espectro de luz emitida, o efeito Doppler permite distinguir que
são estrelas duplas. Esta situação está
esboçada na Fig. 5.5.
(ii) Expansão do universo: as estrelas têm uma
velocidade de fuga de 10-30 km/s e os quasares de aproximadamente
0.8 c. Isto faz com que os espectros de luz emitidos por elementos
químicos conhecidos tenham um deslocamento na direção
do vermelho.
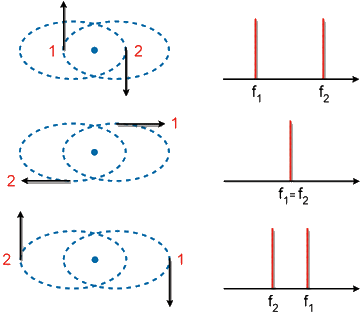
Fig. 5.5 - Efeito Doppler-Fizeau no caso das estrelas duplas.
Sergio Carlos Zilio
|