Como vimos no capítulo anterior, a onda eletromagnética é caracterizada por uma fase que possui dependência nas coordenadas espaciais e temporal, f = f(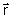,t). Esta grandeza é a característica mais importante da onda eletromagnética já que define a direção de propagação, através do gradiente da função eikonal (vide Cap. 2), a frequência e também sua velocidade de propagação. No presente capítulo vamos concentrar nossa atenção nos aspectos ligados à frequência e velocidade da onda, e como proceder para transmitir informações através dela.

De acordo com o exposto no Cap. 4, as coordenadas espaciais e temporal das fases das ondas analisadas estão separadas em dois termos, da forma 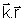- wt. Entretanto, pode acontecer o caso em que estas coordenadas estão misturadas, e um exemplo disto é quando o índice de refração depende do tempo. Como k é proporcional a n, a fase passa a ser f(r,t) = 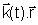- wt, que é conhecida como fase generalizada. A frequência da onda estará então associada à variação temporal da fase generalizada, tópico que veremos com mais detalhes quando tratarmos da modulação eletro-óptica e varredura de frequência. Por enquanto, vamos concentrar nossa atenção na velocidade de propagação da onda. Começaremos por dizer que quando se deseja transmitir sinais, é impossível fazê-lo através de uma onda de frequência única (monocromática), porque os detetores existentes medem a intensidade do sinal e não a fase. Para tal fim, devemos modular a onda, como explicado a seguir.

Vamos considerar duas ondas planas monocromáticas, de frequências w + Dw e w - Dw, propagando-se ao longo da direção z, com os correspondentes vetores de onda k + Dk e k - Dk. Aplicando o princípio da superposição introduzido por Young, temos:

(5.1)

Através de uma manipulação matemática simples desta equação chegamos a:

(5.2)

Como usualmente feito nos livros de eletromagnetismo, tomamos apenas a parte real desta expressão, o que nos leva a:

(5.3)

Isto nos dá uma onda de frequência modulada por outra, de frequência , como mostra a Fig. 5.1.

Fig. 5.1 - Modulação da amplitude da onda.

De acordo com a equação anterior, vemos que a onda portadora, de frequência maior, tem a forma cos(kz-wt) e a modulação é dada por cos(Dkz-Dwt). Vamos concentrar nossa atenção nos pontos A e B, que são respectivamente máximos da modulação e da onda portadora, e determinar as velocidades com que estes pontos se propagam. Estes máximos satisfazem as condições:

onde m e n são inteiros. Diferenciando z com relação a t nas expressões acima obtemos:

que são respectivamente as velocidade da modulação e da onda portadora. A velocidade da onda portadora leva o nome de velocidade de fase e a da modulação o de velocidade de grupo. Neste caso em que temos duas ondas monocromáticas, o espectro de frequências é composto por duas "funções delta". Para o caso de um "pacote" ou grupo de ondas cujo espectro de frequências é uma função caixa, como mostra a Fig. 5.2, teremos que somar (integrar) todas as componentes de frequências para encontrar a expressão do campo elétrico como fizemos para as duas ondas monocromáticas na eq. (5.1). Assim,

(5.6)

Fig. 5.2 - Espectro de frequências tipo caixa.

Para efetuar esta integração devemos levar em conta que pode haver dispersão do pacote, isto é, k pode ser uma função w de como veremos quando tratarmos a interação entre a luz e a matéria no Cap. 11. Vamos então expandir k em torno de w₀, de acordo com:

(5.7)

Desprezando termos de ordens superiores à linear em temos:

(5.8)

Fazendo a substituição W = w - w₀ obtemos:

(5.9)

O primeiro termo desta expressão representa a onda portadora e o segundo é a função forma ou modulação que passaremos a chamar g(z,t). Assim,

(5.10)

onde 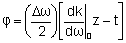. A Fig. 5.3 mostra o pacote de ondas obtido através das equações (5.9) e (5.10).

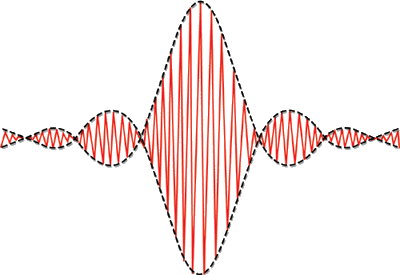
Fig. 5.3 - Pacote de ondas correspondente ao espectro de frequências tipo caixa.

O valor máximo do pacote de ondas ocorre quando f = 0, ou seja, quando 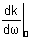z = t. A velocidade com que o pacote se propaga, que é a já conhecida velocidade de grupo, é:

(5.11)

Se houvéssemos tomado o termo de ordem quadrática na expansão de k, obteríamos a dispersão do pacote, isto é, ele mudaria de forma ao se propagar. O conhecimento de como um pacote se dispersa é de muita importância nas telecomunicações, em particular, quando se pretende transmitir uma sequência de pulsos curtos numa fibra óptica. Se a taxa de repetição for alta, os pulsos estarão muito próximos e poderão se superpor, produzindo confusão na informação que está sendo transmitida. Deixaremos a análise da dispersão de um pulso como exercício, mas vamos mencionar aqui que esta dispersão da velocidade de grupo pode ser cancelada por um efeito não linear de terceira ordem chamado varredura de frequência. Isto dá origem ao sóliton temporal que veremos na seção 5.6.

Além da dispersão devido à variação do índice de refração com a frequência, que acabamos de ver, existe um outro tipo de dispersão nas fibras ópticas, chamada de dispersão modal. Cada um dos modos transversais mostrados na Fig. 4.9 possui uma velocidade de propagação diferente. Se o pulso de luz constituir-se de uma soma destes modos, cada um deles caminhará com velocidade diferente, acarretando no alargamento do pulso. Para evitar esta complicação, costuma-se usar para as comunicações ópticas fibras mono-modos que permitem a propagação apenas do modo TEM₀₀.

Sergio Carlos Zilio