|
Uma
solução importante da equação de ondas
é aquela obtida ao se utilizar o Laplaceano em coordenadas
cilíndricas:
onde
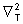é a parte associada à coordenada radial. Fisicamente,
o uso destas coordenadas implica que o meio possui condições
de contorno com simetria azimutal, isto é, podem existir obstáculos
circulares, meios do tipo lente como discutido no Cap. 2, etc. A solução
que vamos obter a seguir é de observação bastante
comum em laboratórios de óptica, pois corresponde ao
tipo de luz emitida pela maioria dos lasers. Como o sistema de coordenadas
particulares escolhido para o Laplaceano não tem influência
na parte temporal do campo elétrico, é de se esperar
que, como nos dois casos discutidos na seção anterior,
ele seja dado por uma expressão do tipo:
Substituindo
esta solução tentativa na eq. (4.5), obtemos a equação
de ondas na forma reduzida, que envolve apenas as coordenadas espaciais:
onde
k2 = mew2
pode depender da coordenada radial se tivermos um meio do tipo lente.
Entretanto, com o objetivo de simplificar os cálculos seguintes,
vamos supor que o meio seja homogêneo, isto é, k é
constante. Tomando apenas uma componente vetorial de
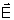e supondo que a onda tem sua propagação confinada em
torno do eixo z, fazemos a mudança de variáveis:
que
quando substituida na eq. (4.15) resulta em:
onde
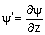e o termo proporcional a
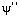foi desprezado. Esta é ainda uma equação difícil
de ser resolvida e sem nenhuma justificativa ad hoc, vamos tentar
uma solução do tipo:
Substituindo
na eq. (4.23) obtemos:
onde
as derivadas de P e Q são relativas a z. Como esta igualdade
é válida para qualquer r, devemos analisar as partes
que possuem a mesma potência em r. Assim,
Desta
forma, obtemos equações diferenciais, que embora não
lineares, são de primeira ordem, e consequentemente fáceis
de serem resolvidas. A solução da eq. (4.26a) resulta
em:
onde
q0 é uma constante de integração, que
será analisada posteriormente. Utilizando este resultado na
eq. (4.26b) é fácil mostrar que:
Podemos
agora substituir os valores de P(z) e Q(z) na eq. (4.24) para encontrarmos
a função y(r,z). Antes porém,
vamos re-escrever a constante de integração como q0
= iz0, com z0
real. A razão de se considerar q0
imaginário é que esta é a única maneira
de se obter uma solução que está confinada em
torno do eixo z; caso contrário, o campo elétrico se
estenderia exponencialmente até o infinito e esta é
uma solução que não nos interessa. Desta forma
temos:
onde
as grandezas w(z) e R(z) foram introduzidas como:
onde
w0 = 2z0/k é o valor de w(z) na origem (z =
0) e
Com
estas definições o campo elétrico fica:
onde
h(z) = tg-1(z/z0). Podemos agora fazer uma interpretação
do significado desta expressão. A primeira parte da eq. (4.32)
está ligada à amplitude do campo. Vemos que ao se modificar
a coordenada radial o campo decai exponencialmente, de forma a seguir
uma função gaussiana. O comportamento de E contra r
está mostrado na Fig. 4.7. Para uma distância r =
w(z), o valor de E decai para 1/e do valor em r =
0. Esta distância é chamada de raio do feixe. Na origem,
o raio mínimo é w0,
de acordo com a eq. (4.31a). Nesta posição temos a "cintura
do feixe". Ainda de acordo com esta equação, vemos que
z0= kw02/2 = nw02/l. Este parâmetro é chamado de intervalo de
Rayleigh. Para z = z0, o raio do feixe aumenta de um fator
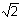quando comparado com o valor em r = 0.
Ainda com relação à amplitude do campo, para
r = 0, o feixe vai se abrindo conforme z aumenta e a amplitude
decai com z, de acordo com w0/w(z)=
 .
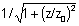É interessante notar que existe um tamanho mínimo para
o diâmetro do feixe e isto está ligado ao fenômeno
de difração, que veremos no Cap. 9. Para z muito maior
que z0, a eq. (4.31a) prediz que w(z)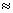 
w0z/z0. Usando a relação
entre w0 e z0,
e considerando que o diâmetro do feixe satisfaz r =
w(z), temos:
que
é a equação de uma reta, que nos dá o
ângulo de divergência do feixe como tgq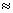
q = l/pnw0. Iremos obter uma expressão similar a esta quando
tratarmos da difração de luz por um fenda circular de
raio w0.
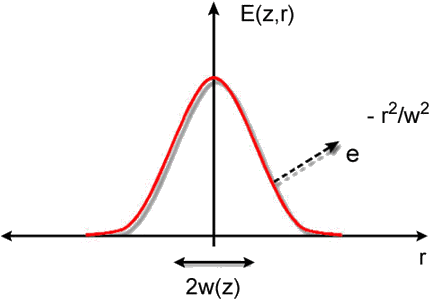
Fig. 4.7 - Variação da amplitude do campo com a coordenada
radial.
A
segunda metade da eq. (4.32) está ligada à fase da onda.
O termo mais interessante é o que possui R(z), que corresponde
ao raio de curvatura da frente de onda, como discutido na seção
3.5. Quando a onda se propaga, a curvatura do feixe vai mudando conforme
mostra a Fig. 4.8. Para r = 0 e r = 
o raio de curvatura é infinito. O valor mínimo de R(z)
ocorre para z =
z0 e vale Rmin
= 2z0. Par z < 0, o
raio de curvatura é positivo e se a luz caminha para a direita
temos a divergência do feixe. Por outro lado para z 0, o raio
de curvatura é negativo e o feixe estará convergindo.
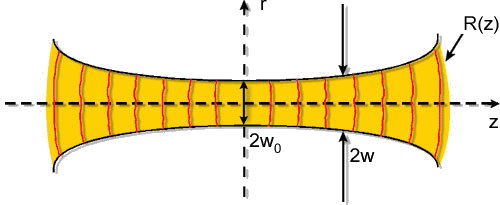
Fig. 4.8 - Propagação de um feixe gaussiano (a) e
variação da amplitude do campo com coordenada radial.
O
feixe definido pela eq. (4.32) é chamado feixe gaussiano de
ordem zero (TEM00), podendo existir
feixes de ordem superior, cujas distribuições de intensidade
na direção radial são mostrados na Fig. 4.9.
Embora não demonstremos aqui, a amplitude do campo elétrico
é modulada por um polinômio de Hermite. Alguns pontos
a serem enfatizados com relação à eq. (4.32)
são: (i) o raio da curvatura R(z) e o diâmetro do feixe
mudam conforme ele se propaga na direção z, implicando
numa divergência (ou convergência) do mesmo, (ii) em w(z)
o campo é 1/e do valor em r = 0,
(iii) o parâmetro confocal z0
= pw02n/l é a distância
z em que o raio w(z) do feixe aumenta por um fator
,
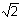(iv) w0 é o raio mínimo do feixe, obtido no ponto
focal e (v) a propagação do
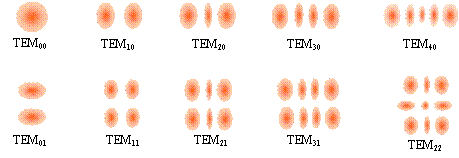
Fig. 4.9 - Distribuições transversais de intensidade
para
feixes gaussianos de várias ordens.
feixe
não segue as leis da óptica geométrica devido
à difração da luz no ponto focal, mas pode ser
descrita através de matrizes (lei ABCD), como discutido na
referência 4.3, e na seção seguinte.
Sergio Carlos Zilio
|
