| |

O
caso discutido acima é o das ondas harmônicas uni-dimensionais,
para as quais a propagação ocorre apenas ao longo do
eixo z. No caso de uma onda que se propaga numa direção
qualquer do espaço, além de z, as coordenadas x e y
também aparecem na solução da equação
de ondas se utilizarmos o Laplaceano em coordenadas cartesianas. Assim,
generalizando a eq. (4.11) temos:
onde
o vetor
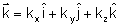 define a direção de propagação da onda
e é chamado de vetor de propagação, cujo módulo,
como já vimos é 2p/l.
define a direção de propagação da onda
e é chamado de vetor de propagação, cujo módulo,
como já vimos é 2p/l.
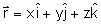 é chamado de vetor posição. Os versores é chamado de vetor posição. Os versores
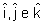 indicam a direção e sentido dos eixos x, y e z,
do sistema de coordenadas cartesianas. A solução dada
por (4.14) é de extrema importância uma vez que qualquer
pulso indicam a direção e sentido dos eixos x, y e z,
do sistema de coordenadas cartesianas. A solução dada
por (4.14) é de extrema importância uma vez que qualquer
pulso
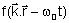 pode ser gerado fazendo uma superposição de campos elétricos
E(w), isto é, calculando a transformada de Fourier
de E0(w):
pode ser gerado fazendo uma superposição de campos elétricos
E(w), isto é, calculando a transformada de Fourier
de E0(w):
sendo
que w0 entra nos limites de
integração. Desta forma podemos ver que a solução
harmônica é uma espécie de onda básica
e as soluções mais complicadas são derivadas
a partir dela. Voltaremos a este assunto no Cap. 8, quando estudarmos
a resolução espectral de um trem de ondas finito. Entretanto,
devemos afirmar que embora esta solução seja importante
do ponto de vista matemático, ela não tem significado
físico, já que as condições de contorno
demandariam fontes de dimensões infinitas (planos), como veremos
a seguir.
De
acordo com a eq. (4.14), a fase da onda é f(r,t)=
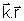 - wt. Vamos
encontrar para quais pontos no espaço esta fase tem o mesmo
valor, isto é, queremos determinar as superfícies equifases.
Assim, para um dado instante de tempo f
deve ser constante e isto só é possível se - wt. Vamos
encontrar para quais pontos no espaço esta fase tem o mesmo
valor, isto é, queremos determinar as superfícies equifases.
Assim, para um dado instante de tempo f
deve ser constante e isto só é possível se
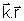 = =
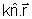 = constante. Aqui,
= constante. Aqui,
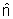 é um versor que especifica a direção e o sentido
do vetor de propagação
é um versor que especifica a direção e o sentido
do vetor de propagação
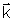 .
A realização do produto escalar nos leva a: kxx + kyy + kzz
= constante, que é a equação
do plano visto na Fig. 4.3, cuja normal é o próprio
vetor de propagação. Desta forma concluimos que a onda
plana possui como superfícies equifases, planos que se propagam
na direção de .
A realização do produto escalar nos leva a: kxx + kyy + kzz
= constante, que é a equação
do plano visto na Fig. 4.3, cuja normal é o próprio
vetor de propagação. Desta forma concluimos que a onda
plana possui como superfícies equifases, planos que se propagam
na direção de 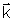 ,
com velocidade v. ,
com velocidade v.
Para entendermos melhor o significado de
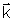 vamos fazer uso da Fig. 4.4, que representa duas superfícies
equifases tais que os argumentos das funções seno diferem
exatamente de 2p, significando que a onda se repete. Logo, a separação
entre os dois planos é l, como discutido anteriormente. Assim, para um certo tempo
t, vamos fazer uso da Fig. 4.4, que representa duas superfícies
equifases tais que os argumentos das funções seno diferem
exatamente de 2p, significando que a onda se repete. Logo, a separação
entre os dois planos é l, como discutido anteriormente. Assim, para um certo tempo
t,
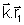 - wt = const. e
- wt = const. e
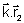 - wt= const.+2p. Subtraindo estas
duas igualdades temos: - wt= const.+2p. Subtraindo estas
duas igualdades temos:
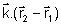 = 2p. Levando
em conta que o produto escalar seleciona apenas a componente = 2p. Levando
em conta que o produto escalar seleciona apenas a componente
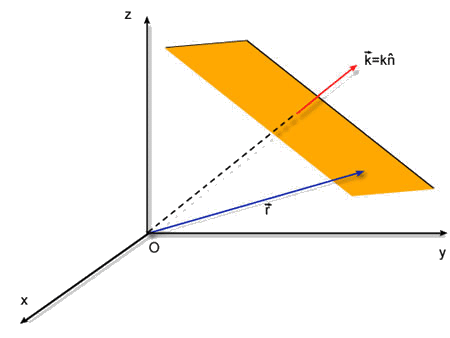
Fig. 4.3 - Superfície equifase de uma onda plana.
de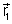 paralela a
paralela a 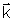 (portanto perpendicular aos planos equifases), e que esta corresponde
à separação entre os dois planos consecutivos,
concluímos que kl = 2p e consequentemente k = 2p/l , como no caso da onda unidimensional.
Como para a translação com velocidade constante, o espaço
é igual à velocidade vezes o tempo, temos l
= Tv = v/f. Assim obtemos v =
lf = w/k, que é a velocidade de fase da onda, que será
abordada com maiores detalhes no final do capítulo.
(portanto perpendicular aos planos equifases), e que esta corresponde
à separação entre os dois planos consecutivos,
concluímos que kl = 2p e consequentemente k = 2p/l , como no caso da onda unidimensional.
Como para a translação com velocidade constante, o espaço
é igual à velocidade vezes o tempo, temos l
= Tv = v/f. Assim obtemos v =
lf = w/k, que é a velocidade de fase da onda, que será
abordada com maiores detalhes no final do capítulo.
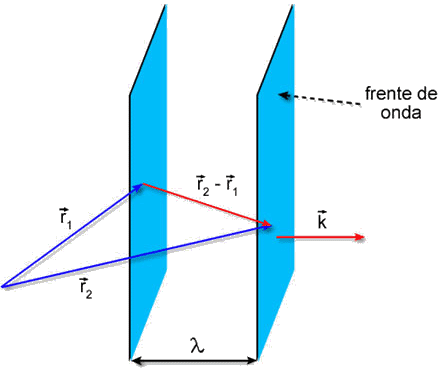
Fig. 4.4 - Significado de .
Um
outro tipo de solução para a equação de
ondas é a onda esférica, que está ligada à
condição de contorno correspondente à radiação
emitida por uma fonte pontual. Quando tal fonte emite radiação
eletromagnética, a onda gerada se espalha em todas as direções,
como mostrado na Fig. 4.5, diferentemente da onda plana que caminha
apenas na direção do vetor de propagação
 .
Neste caso, o campo elétrico é dado por: .
Neste caso, o campo elétrico é dado por:
Nesta
expressão vemos que a amplitude decresce com r e a razão
para isto está ligada ao princípio da conservação
de energia. A potência (energia por unidade de tempo) é
o produto da intensidade pela área atravessada pela onda, que
no caso da esfera é A = 4pr2. Logo, devido à conservação de energia
(ou potência), 4pr2I deve ser constante
conforme a onda esférica se propaga. Como veremos no final
do capítulo, I
 E2 (ver eq. (4.41)) de onde
concluimos que E depende de 1/r. Conforme mostra a Fig. 4.5, o produto
kr dá origem a uma superfície equifase esférica,
dependente de r. Note que no argumento da exponencial aparecem apenas
os módulos dos vetores E2 (ver eq. (4.41)) de onde
concluimos que E depende de 1/r. Conforme mostra a Fig. 4.5, o produto
kr dá origem a uma superfície equifase esférica,
dependente de r. Note que no argumento da exponencial aparecem apenas
os módulos dos vetores
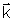 e
e
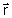 ,
e não o seu produto escalar. ,
e não o seu produto escalar.
Fig. 4.5 - Onda esférica.
Existem
outros tipos de soluções para a equação
de ondas e um dos mais comuns é a solução do
tipo gaussiana, que abordaremos na seção 4.5.
Uma identidade importante é a que relaciona
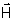 e
e
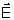 .
Para derivá-la devemos notar que de acordo com a expressão
da onda plana, .
Para derivá-la devemos notar que de acordo com a expressão
da onda plana,
Como
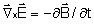 =
=
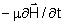 ,
temos ,
temos
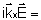
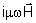 ,
isto é, ,
isto é,
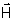 e
e
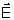 são perpendiculares entre si. Por outro lado,
são perpendiculares entre si. Por outro lado,
significando
que 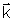 e
e 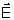 são perpendiculares. Também,
são perpendiculares. Também,
e
assim,
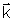 e
e
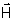 são perpendiculares. Logo, concluímos que
são perpendiculares. Logo, concluímos que
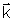 , ,
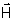 e e
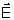 são mutuamente perpendiculares, como mostra a Fig. 4.6. É
claro que isto só é válido em meios isotrópicos,
onde
são mutuamente perpendiculares, como mostra a Fig. 4.6. É
claro que isto só é válido em meios isotrópicos,
onde
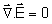 . Nos meios anisotrópicos, a condição a ser
utilizada é . Nos meios anisotrópicos, a condição a ser
utilizada é
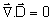 ,
e neste caso, ,
e neste caso,
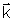 , ,
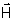 e
e
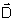 são mutuamente perpendiculares.
são mutuamente perpendiculares.
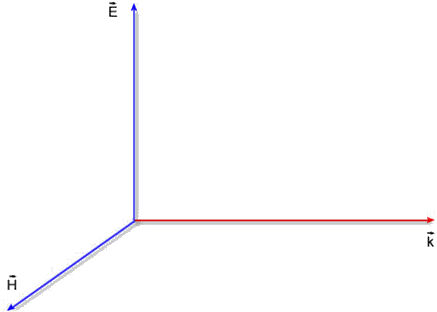
Fig. 4.6 - Geometria dos vetores
Sergio Carlos Zilio
|
|