| |

A equação para a onda eletromagnética unidimensional tem a forma da
equação para u e portanto, sua solução se constitui de pulsos do tipo:
E
= E(z
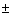 vt) vt)
H
= H(z 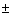 vt) vt)
|
|
caminhando com velocidade
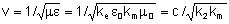 ,
onde c é a velocidade da luz no vácuo (ke = km =1). Para meios dielétricos
e não magnéticos (km =1), temos ,
onde c é a velocidade da luz no vácuo (ke = km =1). Para meios dielétricos
e não magnéticos (km =1), temos
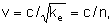 onde n =
onde n =
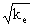 é o índice de refração do meio.
é o índice de refração do meio.
Um caso particular muito interessante das soluções expressas pelas
eq. (4.8a) e (4.8b) é o das ondas harmônicas, que são perturbações
periódicas da forma:
onde definimos:
sendo a freqüência angular da onda e k a constante de propagação ou
módulo do vetor de propagação. Posteriormente, veremos com mais
detalhes o significado físico destas grandezas. Assim como a expressão
co-senoidal apresentada acima, soluções do tipo seno também satisfazem
a equação de ondas e também são chamadas de ondas harmônicas. Como
exemplo, no caso das ondas mecânicas funções do tipo seno ou co-seno
podem ser obtidas conectando um diapasão numa das extremidades de uma
corda esticada. Existe ainda uma terceira maneira de se expressar a
onda harmônica, mais conveniente para a realização da operação de
multiplicação dos campos, que é a forma exponencial:
que também satisfaz a equação de ondas. De acordo com a forma de Euler
(exp{iq}= cosq + i senq ) esta expressão contém um termo real e outro
imaginário. Como o campo elétrico (assim como o magnético) deve ser
uma variável real, é costume tomar-se apenas a parte real (ou
imaginária) da eq. (4.11).
Vamos enfatizar aqui que uma onda tem três partes importantes: a) a
amplitude (Eo), b) a orientação
espacial dos campos (polarização) e c) a fase (kz 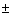 wt). A amplitude está ligada à
intensidade, que determina a potência que está sendo transportada pela
onda. A polarização dos campos está vinculada à orientação do vetor
campo elétrico no espaço. Esta orientação define o que chamamos de
polarização de uma onda e será tema de muitas discussões ao longo do
texto, como por exemplo, quando estudarmos os fenômenos de reflexão e
refração. Veremos ainda que a fase, que é o argumento da função que
descreve a onda, é um elemento fundamental no entendimento de vários
fenômenos, como por exemplo o da interferência de ondas.
wt). A amplitude está ligada à
intensidade, que determina a potência que está sendo transportada pela
onda. A polarização dos campos está vinculada à orientação do vetor
campo elétrico no espaço. Esta orientação define o que chamamos de
polarização de uma onda e será tema de muitas discussões ao longo do
texto, como por exemplo, quando estudarmos os fenômenos de reflexão e
refração. Veremos ainda que a fase, que é o argumento da função que
descreve a onda, é um elemento fundamental no entendimento de vários
fenômenos, como por exemplo o da interferência de ondas.
O argumento das funções dadas nas eq. (4.8a) e (4.8b) possui um
termo descrevendo a variação espacial da onda, e outro, a temporal. De
fato, não é algo simples a visualização conjunta das variações no
espaço e no tempo, e a maneira mais funcional para analisar a fase é
fazê-la separadamente. Para simplificar ainda mais a discussão,
faremos uso das ondas harmônicas definidas nas eq. (4.9a) e (4.9b).
Vamos somar 2 ao argumento da função, o que não altera o valor da
amplitude do campo da onda pois cos f
= cos (f+2p). Ao fazermos este
incremento de fase, sua origem pode ser oriunda tanto da parte
espacial quanto temporal, isto é, a variação pode ser no valor de z ou
no de t.
Tomemos inicialmente a variação de fase como sendo de origem
temporal. Consideremos um dado instante de tempo t e que decorrido um
intervalo de tempo T, a fase se altera como um todo de 2p.
Desta forma, temos:
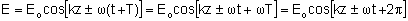 .
Neste caso, wT = 2p que nos leva a: .
Neste caso, wT = 2p que nos leva a:
O intervalo de tempo T para o qual a onda harmônica se repete é
chamado de período temporal da onda. A eq. (4.12) define a relação que
deve existir entre período, freqüência angular w
e freqüência f.
Tomemos a seguir a variação de 2p na fase
como sendo oriunda da parte espacial. Desta forma, consideramos a onda
em um dado ponto z e, no mesmo instante, o ponto (z+l), tal que este deslocamento espacial gere a variação de
fase citada. Temos então que
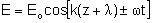
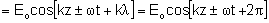 .
Disto vem que kl = 2p e consequentemente: .
Disto vem que kl = 2p e consequentemente:
Portanto, chegamos à conclusão que existe um período espacial dado
por , à semelhança do período temporal já discutido. A eq. (4.13)
define a relação entre o módulo do vetor de propagação e este período
espacial, chamado de comprimento de onda. Isto evidencia que as partes
espacial e temporal de uma onda participam em pé de igualdade, ou
seja, tanto é possível haver alteração de uma onda através da passagem
do tempo quanto da mudança de posição no espaço. A Fig. 4.2 ilustra o
comportamento de uma onda harmônica como função da variável espacial
para diversos tempos, isto é, como se a onda fosse fotografada
periodicamente. A mudança de uma onda no tempo é algo muito comum em
eletrônica, enquanto que a mudança de fase no espaço é algo próprio da
óptica. Assim sendo, em eletrônica se faz a modulação de sinal no
tempo, enquanto em óptica se pode modular não apenas no tempo, mas
também no espaço.

Fig. 4.2 - Evolução temporal-espacial de uma onda harmônica.
Conforme o tempo passa, a onda caminha para a direita com velocidade
v constante
Sergio Carlos Zilio
|
|