| |

Por
volta de 1870, James Clerk Maxwell introduziu um conjunto de equações
envolvendo os campos elétrico e magnético, colocando
de forma clara as equações empíricas existentes
na época. Também introduziu o conceito de corrente de
deslocamento, tornando a lei de Ampère mais geral. Estas equações,
conhecidas atualmente como equações de Maxwell, estão
discutidas em detalhes nos textos básicos de eletromagnetismo
(ver referência 4.1). Temos:
| |
(4.3a)
(4.3b)
(4.3c)
(4.3d)
|
onde
o sistema internacional (MKSA) foi adotado. O último termo
da eq. (4.3d) representa a corrente de deslocamento introduzida por
Maxwell. Cada uma destas equações corresponde a uma
lei física descoberta empiricamente. De acordo com a ordem
usada acima temos: lei de Gauss, inexistência de monopolo magnético,
lei da indução de Faraday e lei de Ampère-Maxwell.
O significado das grandezas que aparecem neste conjunto de equações
é o usual:
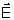 é o campo elétrico,
é o campo elétrico,
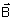 é a indução magnética, r é a densidade de portadores livres, é a indução magnética, r é a densidade de portadores livres,
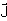 é a densidade de corrente devida aos portadores livres,
é a densidade de corrente devida aos portadores livres,
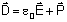 é o deslocamento elétrico e é o deslocamento elétrico e
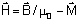 é o campo magnético. Introduzimos assim, a polarização
elétrica e a magnetização , que correspondem
à resposta do meio devido à presença dos campos
elétrico e magnético, respectivamente. As constantes
e0 = 8.854x10-12
F/m e m0
= 4 x10-7
H/m, determinadas empiricamente, são denominadas respectivamente
de permissividade e permeabilidade do vácuo.
é o campo magnético. Introduzimos assim, a polarização
elétrica e a magnetização , que correspondem
à resposta do meio devido à presença dos campos
elétrico e magnético, respectivamente. As constantes
e0 = 8.854x10-12
F/m e m0
= 4 x10-7
H/m, determinadas empiricamente, são denominadas respectivamente
de permissividade e permeabilidade do vácuo.
As equações de Maxwell podem ser combinadas de forma
a gerar uma nova equação que descreve a onda eletromagnética.
Antes porém, vamos fazer hipóteses simplificadoras para
as relações constitutivas que nos dão a resposta
do meio à presença dos campos. Vamos supor relações
lineares do tipo
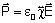 , ,
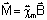 e
e
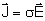 (conhecida como lei de Ohm), onde
(conhecida como lei de Ohm), onde
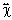 e
e
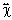 m
são respectivamente as susceptibilidades elétrica e
magnética e s é a condutividade
elétrica. Em geral m
são respectivamente as susceptibilidades elétrica e
magnética e s é a condutividade
elétrica. Em geral
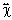 é um tensor, de forma que as polarizações e os
campos podem não ser paralelos. Entretanto, neste capítulo
vamos considerar apenas meios isotrópicos, nos quais
é um tensor, de forma que as polarizações e os
campos podem não ser paralelos. Entretanto, neste capítulo
vamos considerar apenas meios isotrópicos, nos quais
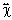 e
e
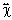 m
são escalares, isto é, m
são escalares, isto é,
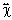 ij
= ij
=
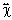 dij.
Voltaremos a abordar o caráter tensorial destas grandezas quando
tratarmos da propagação da luz em meios anisotrópicos
dentre os quais se enquadram diversos tipos de cristais. Desta forma, dij.
Voltaremos a abordar o caráter tensorial destas grandezas quando
tratarmos da propagação da luz em meios anisotrópicos
dentre os quais se enquadram diversos tipos de cristais. Desta forma,
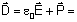
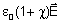
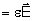 ,
onde ,
onde
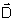 e
e
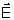 são paralelos. Analogamente,
são paralelos. Analogamente,
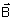 = m
= m
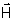 ,
onde m = m0 (1+ cm). Definiremos constante dielétrica como ke
= e/e0 = (1+ c) e permeabilidade magnética
como km = m/m0
= (1+ cm). ,
onde m = m0 (1+ cm). Definiremos constante dielétrica como ke
= e/e0 = (1+ c) e permeabilidade magnética
como km = m/m0
= (1+ cm).
Estamos interessados em estudar a propagação de ondas
eletromagnéticas num meio livre e homogêneo, isto é,
r =
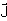 = 0, m e e
não dependem da posição. Tomando-se o rotacional
da eq. (4.3c) temos:
= 0, m e e
não dependem da posição. Tomando-se o rotacional
da eq. (4.3c) temos:
Usando a eq. (4.3d) com 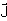 = 0, a identidade vetorial
= 0, a identidade vetorial
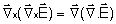 e
e
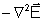 o fato que num meio livre e homogêneo,
o fato que num meio livre e homogêneo,
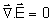 ,
obtemos a equação de ondas: ,
obtemos a equação de ondas:
Analogamente, tomando o rotacional da lei de Ampère-Maxwell
e usando as eq. (4.3b) e (4.3c), obtemos uma equação
similar para o campo magnético:
Se
considerarmos a propagação em apenas uma dimensão
(apenas na direção z, por exemplo), o Laplaceano se
transforma numa derivada segunda com relação a z, e
assim as eq. (4.5) e (4.6) tem a forma da equação de
ondas dada por (4.1). Este tipo de equação já
era conhecido na época, de forma que Maxwell pode concluir
que se tratava de uma onda com velocidade de propagação
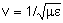 .
É interessante enfatizar que quando estas equações
foram obtidas pouco se conhecia sobre a natureza da luz. Apenas quando
Maxwell substituiu os valores de e , conhecidos empiricamente através
de medidas de capacitância e indutância, obteve-se que
a onda eletromagnética tinha uma velocidade de propagação
igual à da luz, e assim pode ser feito o relacionamento entre
a óptica e o eletromagnetismo. No caso tridimensional, as equações
(4.5) e (4.6) são cada uma um conjunto de três equações
para as componentes, isto é: .
É interessante enfatizar que quando estas equações
foram obtidas pouco se conhecia sobre a natureza da luz. Apenas quando
Maxwell substituiu os valores de e , conhecidos empiricamente através
de medidas de capacitância e indutância, obteve-se que
a onda eletromagnética tinha uma velocidade de propagação
igual à da luz, e assim pode ser feito o relacionamento entre
a óptica e o eletromagnetismo. No caso tridimensional, as equações
(4.5) e (4.6) são cada uma um conjunto de três equações
para as componentes, isto é:
Existe
ainda um conjunto de equações similares para o campo
magnético. Todas são equações diferenciais
lineares, de segunda ordem, que podem ter uma infinidade de soluções,
dependendo das condições de contorno impostas pela geometria
de cada situação particular. Na seção
seguinte vamos discutir os tipos de soluções mais comuns.
Sergio Carlos Zilio
|
|