Para entendermos a propagação de uma onda e outros aspectos físicos relacionados à luz vamos inicialmente rever algumas idéias ligadas ao conceito de onda. Começaremos analisando uma onda mecânica, que é uma perturbação que caminha num meio material. Um exemplo bastante conhecido é o de uma corda estirada no chão sobre a qual se exerce um rápido puxão para cima. Sabemos que se forma um pulso nesta corda e que ele caminha (ou propaga-se) ao longo dela. Esta situação corresponde ao caso de propagação em uma dimensão (direção), ilustrado na Fig. 4.1. Outro exemplo de onda mecânica é o caso de uma pedra que cai na superfície absolutamente calma de um lago. Ao tocar na água, a pedra provoca um movimento do líquido, na forma de um círculo que aumenta radialmente. Neste caso, temos uma onda que se propaga em duas dimensões, sobre o plano definido pela superfície do lago. Estes são exemplos de perturbações que podem ser caracterizados como movimentos ondulatórios chamados pulsos.

Fig. 4.1 - Ilustração de um pulso propagando-se numa corda.

Uma pergunta pertinente seria: podemos descrever este efeito matematicamente? A resposta é obviamente sim e a equação que descreve a propagação da onda, bem como sua solução, já eram conhecidas desde o século XVIII. Se estivermos tratando com ondas unidimensionais, que caminham apenas na direção z, por exemplo, a equação que descreve sua propagação é dada por:

(4.1)

que envolve derivadas parciais de segunda ordem com relação às variáveis espaço e tempo. A função u representa a perturbação provocada pela onda no meio, como por exemplo, a altura do pulso na corda. Por sua vez, v é a velocidade com que a onda caminha. Esta equação diferencial tem como soluções possíveis quaisquer funções que possuam o argumento descrevendo um movimento retilíneo uniforme, dado por: z = z₀ 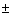vt, ou alternativamente, z 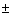vt = constante. Nesta última expressão, o sinal negativo corresponde a um movimento na direção do eixo z, enquanto que o sinal positivo descreve um movimento na direção negativa do eixo z. Estas soluções referem-se às ondas que se propagam sem dispersão, isto é, o pulso caminha com velocidade constante, sem que haja distorção no seu formato. No Cap. 5 trataremos do caso mais geral em que existe dispersão, a qual provoca mudanças no formato do pulso ao se propagar.

Uma onda pode ser descrita de maneira geral como: u₁ = f (z-vt) e u₂ = g (z+vt), onde f e g são funções quaisquer. Se houver no meio ondas se propagando simultaneamente nas duas direções, a solução geral é dada pela combinação linear:

(4.2)

onde u₁ e u₂ representam respectivamente, pulsos caminhando nas direções +z e -z. A combinação linear das ondas presentes no meio, expressa pela eq. (4.2), é conhecida como princípio da superposição e será abordada no problema 4.1. A forma de cada pulso é estabelecida pelas funções f e g, e depende das condições iniciais do problema, isto é, de como se gera o pulso no meio. Ao contrário das ondas mecânicas, as ondas eletromagnéticas, que discutimos a seguir, não precisam de um meio material para se propagarem.

Sergio Carlos Zilio