|

Devido à dispersão (dn/dl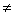 0) dos
vidros utilizados na confecção das lentes, o índice
de refração depende do comprimento de onda e assim,
de acordo com a eq. (3.12), o foco varia com l. Esta variação é chamada de aberração
cromática e pode ser substancialmente reduzida pela combinação
de duas lentes feitas de vidros diferentes de tal maneira que a aberração
de uma compensa a da outra. Este par de lentes é chamado de
dubleto acromático e foi desenvolvido por John Dollond em 1758.
Para entender seu princípio de funcionamento, devemos tomar
a equação do fabricante de lentes, eq. (3.12), e expandir
o índice de refração em torno de um dado comprimento
de onda l0. Assim, 0) dos
vidros utilizados na confecção das lentes, o índice
de refração depende do comprimento de onda e assim,
de acordo com a eq. (3.12), o foco varia com l. Esta variação é chamada de aberração
cromática e pode ser substancialmente reduzida pela combinação
de duas lentes feitas de vidros diferentes de tal maneira que a aberração
de uma compensa a da outra. Este par de lentes é chamado de
dubleto acromático e foi desenvolvido por John Dollond em 1758.
Para entender seu princípio de funcionamento, devemos tomar
a equação do fabricante de lentes, eq. (3.12), e expandir
o índice de refração em torno de um dado comprimento
de onda l0. Assim,
onde Dl = l-l0 e f é o valor
da distância focal no ponto l0. Note que f(l) depende de
ll apenas no termo Dl e as demais grandezas que aparecem na equação
são calculadas no ponto l0.
No caso de um dubleto, temos duas lentes de distâncias focais
f1 e f2 muito próximas, de forma que a eq. (3.17) pode
ser aplicada. Definindo:
como grandezas calculadas no ponto l0, podemos escrever a
distância focal da lente equivalente como:
onde, novamente, a dependência de f em l está contida no termo Dl. A eq. (3.33) pode ser re-escrita como:
onde 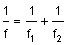 .
Como queremos que f(l) não dependa de
l, o termo entre parênteses deve ser
nulo. Assim, temos duas equações: .
Como queremos que f(l) não dependa de
l, o termo entre parênteses deve ser
nulo. Assim, temos duas equações:
que podem fornecer
os valores desejados de f1 e f2:
Em suma, conhecendo-se a dispersão de um tipo de vidro particular,
computa- se
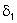 e e
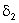 para um dado l0, a partir dos quais
se determina f1 e f2
para o valor de f desejado e constroi-se o dubleto. Entretanto, como
dn/dll também varia com o comprimento
de onda, o dubleto funciona bem apenas num certo intervalo em torno
de l0. Para melhorarmos os
cálculos teríamos que considerar termos de ordens superiores
na expansão dada pela eq. (3.31). para um dado l0, a partir dos quais
se determina f1 e f2
para o valor de f desejado e constroi-se o dubleto. Entretanto, como
dn/dll também varia com o comprimento
de onda, o dubleto funciona bem apenas num certo intervalo em torno
de l0. Para melhorarmos os
cálculos teríamos que considerar termos de ordens superiores
na expansão dada pela eq. (3.31).
Sergio Carlos Zilio
|