No tratamento que empregamos para deduzir as equações da lente supomos a aproximação paraxial, na qual senq e tgq são aproximados pelo argumento q. Esta é uma teoria chamada de primeira ordem. Entretanto, quando um raio passa pela borda da lente, ele é focalizado com um ângulo relativamente grande, de forma que a aproximação paraxial pode não ser boa. Neste caso, mesmo que a luz seja monocromática, de forma que a aberração cromática pode ser ignorada, haverá aberrações de outro tipo. Para entendermos estas aberrações devemos tomar o termo cúbico na expansão do senq e assim passaremos a ter uma teoria de 3a ordem. As diferenças entre esta teoria e a linear são conhecidas como aberrações primárias e são em número de cinco (aberração esférica, coma, astigmatismo, curvatura de campo e distorção). Elas foram estudadas em detalhe por Ludwig von Seidel (1821-1896) por volta de 1850 e por isso levam o nome de aberrações de Seidel. A seguir, descrevemos sucintamente alguns destes tipos de aberrações.

No caso de uma lente simples, o foco efetivo varia com a distância h que o raio incidente entra na lente, de acordo com a Fig. 3.9. Esta variação é chamada de aberração esférica. Para os raios paraxiais (h 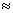0) a eq. (3.12) se aplica e o foco é chamado de foco paraxial.

Fig 3.9 - Aberração esférica produzida por uma lente simples.

Os raios afastados do eixo óptico de uma distância h serão focalizados num outro ponto, chamado de foco periférico, ou marginal, que dista

(3.37)

do foco paraxial, com k sendo dado por:

(3.38)

A aberração esférica será mínima quando a razão entre os raios de curvatura da lente satisfazem:

(3.39)

Esta fórmula só é válida quando o objeto estiver muito afastado da lente (s ). Uma maneira que se usa atualmente para minimizar a aberração esférica é pela construção de lentes cujas superfícies não sejam esféricas (lentes asféricas). As lentes asféricas não são encontradas com facilidade (e são caras). Na prática, o que se pode fazer para minimizar este tipo de aberração, é fazer com que os ângulos de entrada e saída dos raios na lente sejam os mais próximos possíveis. A Fig. 3.10 mostra a maneira de se minimizar a aberração esférica numa lente plano-convexa.

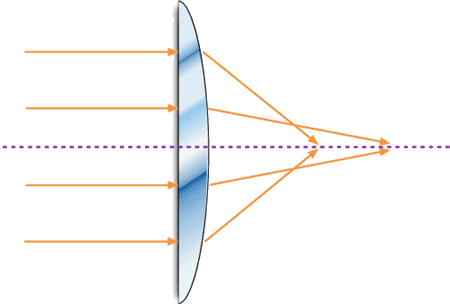
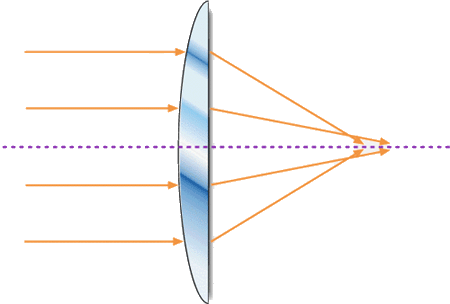
Fig. 3.10 - Aberração esférica de uma lente plano-convexa em duas situações diferentes.

A aberração comática ou simplesmente coma é uma aberração monocromática primária que degrada a imagem e que tem sua origem no fato de que os planos principais só podem ser considerados como planos na aproximação paraxial. Fora desta aproximação, os planos principais são, na verdade, superfícies curvas. A distância focal efetiva e, portanto, a magnificação transversal, será diferente para raios atravessando diferentes regiões fora do eixo da lente, como mostra a Fig. 3.11 para uma fonte pontual. Quando mT diminui para os raios mais externos (como na figura) temos coma negativo e se, mT aumenta, temos coma positivo. Esta aberração apresenta certa analogia com a aberração esférica, pois ambas resultam da impossibilidade de raios paraxiais e marginais convergirem em um mesmo ponto depois de atravessarem a lente. Entretanto, elas se diferenciam na forma da imagem produzida, já que um ponto com aberração esférica resultará numa forma circular e com coma, numa forma de cometa, como mostrado no canto inferior direito da Fig. 3.11.

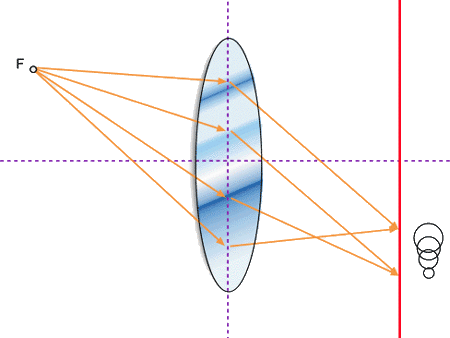
Fig. 3.11 - Exemplo de coma negativo.

A aberração comática depende bastante da posição do objeto e da geometria da lente; entretanto, podemos constatar da Fig. 3.11, que a colocação de uma íris que permita apenas a passagem dos raios pelo centro da lente, diminui bastante este tipo de aberração. Como no caso da aberração esférica, a coma pode ser minimizada ao se escolher adequadamente os raios de curvaturas da lente. Felizmente, a combinação de raios de curvaturas para minimizar a coma é bastante parecida com a combinação para minimizar a aberração esférica.

O astigmatismo, do mesmo modo que a coma, afeta a imagem de um ponto qualquer situado fora do eixo óptico da lente. Considere um feixe de luz colimada incidindo com um ângulo a sobre uma lente. O plano perpendicular ao eixo em torno do qual a lente foi rodada, é chamado de plano meridional enquanto que o plano que contém este eixo é chamado de plano sagital (Fig. 3.12). Obviamente, a simetria dos raios incidente é diferente nestes dois planos e, assim, é de se esperar que as distâncias focais também o sejam. Realmente, encontra-se que no plano meridional o foco é dado por f_m = fcosa enquanto que no plano sagital f_s = f/cosa. Para evitarmos este tipo de aberração, devemos posicionar as lentes de uma montagem experimental sempre perpendiculares aos feixes de luz.

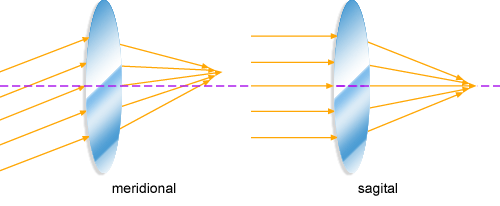
Fig. 3.12 - Os planos meridional e sagital.

Sergio Carlos Zilio