|

Uma lente é classificada como fina quando sua espessura for
muito menor que a distância focal. Existem vários tipos
de lentes cuja denominação depende de sua forma geométrica,
como mostra a Fig. 3.3. Vamos nos ater apenas às lentes de
superfícies esféricas, embora outras simetrias (cilíndrica,
parabólica, elíptica, etc.) sejam hoje em dia de uso
comum. De acordo com o resultado do exercício 3.2, a formação
de imagens por uma lente fina obedece a uma equação
simples:
onde f é a distância focal, s e s’ são respectivamente
as distâncias lente-objeto e lente-imagem. Esta equação
será comprovada na Dem. 3.1.
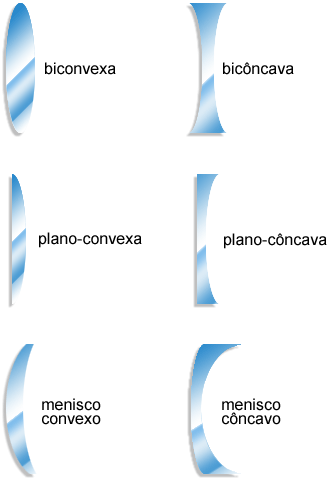
Fig. 3.3 - Seções transversais de algumas lentes finas
de simetria esférica.
É importante para o fabricante de lentes saber como os raios
de curvatura das superfícies esféricas e o índice
de refração do vidro determinam a distância focal
da lente. O relacionamento entre estas grandezas está deduzido
a seguir. Considere uma lente biconvexa formada pelas superfícies
esféricas de raios R1 e R2, como mostrado na Fig. 3.4. O índice
de refração do vidro é n e o do ar é 1.
De acordo com o resultado do exercício 3.4, a matriz que descreve
a interface 1 é dada por:
com R1 > 0 pois o centro de curvatura
C1 encontra-se à direita da
interface, como discutido no exercício 3.4. Similarmente, a
matriz que descreve a interface 2 é dada por:
onde R2 < 0 (centro de curvatura
C2 à esquerda da interface).
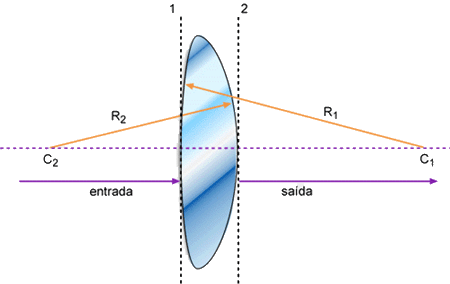
Fig. 3.4 – Seção transversal de uma lente biconvexa
de raios R1 e R2
A matriz que descreve a lente é dada pelo produto M=M2M1 (note a ordem) e resulta em:
Comparando com a matriz da lente positiva, dada pela eq. (3.7), encontramos
a equação do fabricante de lentes:
que é válida na aproximação paraxial para
qualquer tipo de lente fina mostrada na Fig.3.3, tomando-se o cuidado
de respeitar a definição do sinal de R. Uma outra forma
de apresentar a equação do fabricante de lentes é
com o sinal positivo na frente de 1/R2,
porém neste caso a definição do sinal R é
outra: R é positivo se a superfície for convexa e negativo
se for côncava.
Uma propriedade importante da formação de imagens por
uma lente ou espelho é o parâmetro denominado de aumento,
ou magnificação, que caracteriza o tamanho da imagem
em relação ao objeto. De acordo com a Fig. 3.5, podemos
definir a magnificação transversal como:
onde as três últimas igualdades são facilmente determinadas
usando-se geometria elementar. Se mT
> 1, teremos um aumento da imagem em relação ao objeto;
se mT < 1, teremos diminuição da imagem. Os
sinais negativos têm origem na definição dos sinais
de s, s’, x0 e x’0, e no caso
em que mT < 0, significa que a
imagem está invertida.
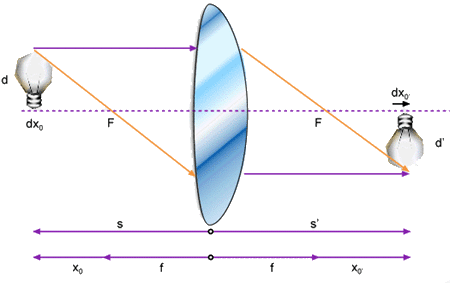
Fig. 3.5 - Formação de imagens por uma lente convergente.
Podemos definir também a magnificação longitudinal
da imagem como:
Para relacionarmos mL com mT tomamos a equação de formação
de imagens (3.8), com s = f + x0 e s’ = f +x0’, de onde
obtemos a forma Newtoniana da equação da lente:
Desta expressão encontramos:
Evidentemente, mL< 0, o que implica
que se dx0 >0 teremos dx0’<0,
ou seja, se o objeto for um dedo apontado para a lente, a imagem será
a de um dedo se afastando da lente.
Sergio Carlos Zilio
|