Neste capítulo daremos sequência ao estudo de óptica geométrica, fazendo uma “revisão” da propagação dos raios através de sistemas ópticos, com ênfase em lentes. Para isto adotaremos um tratamento matemático na forma matricial. Este tipo de formalismo é de muita importância para a descrição da propagação de feixes gaussianos e cálculos de cavidades ressonantes para lasers, como veremos posteriormente. É também adequado para descrever sistemas que incluem muitos elementos ópticos, já que o efeito do conjunto pode ser encontrado através de multiplicação de matrizes.

Vamos levar em conta apenas os raios paraxiais confinados ao redor do eixo óptico (q muito pequeno). Considere a situação mostrada na Fig. 3.1. Podemos supor que, na aproximação paraxial, existe uma relação linear entre as características geométricas dos feixes de entrada e saida do sistema óptico. Desta forma, tomando Y_i como a altura e q_i como o ângulo do raio incidente no sistema óptico, e Y_e e q_e como os parâmetros do feixe emergente, podemos escrever um conjunto de equações envolvendo estas grandezas:

(3.1)

que pode ser colocada na forma matricial:

(3.2)

ou esquematicamente, na notação de Dirac utilizada na mecânica quântica, | 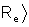= S | 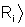. Para um sistema óptico composto de vários elementos, basta apenas fazer a multiplicação de suas matrizes, respeitando a ordem com que os raios incidem nos elementos. Assim, | 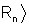= nS_n-1....S₂S₁| .

Como exemplo, vamos encontrar a matriz S para uma lente positiva (convergente) de distância focal f. A Fig. 3.2 mostra os raios principais para uma lente convergente. Note que quando o raio estiver descendo dy/dz<0 e portanto q é negativo.

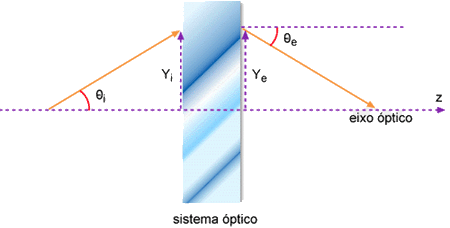
Fig. 3.1 - Raios incidentes e emergentes de um sistema óptico.
Na aproximação paraxial, dy/dz = tgq q.

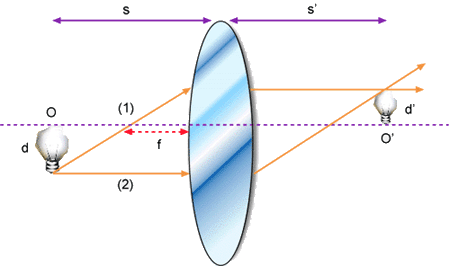
Fig. 3.2 - Traçado de raios para uma lente convergente de distância focal f.
O corresponde ao objeto (tamanho d) e O’ à imagem (tamanho d’).

Vamos usar a aproximação paraxial, na qual d e d’ são muito menores que a distância focal f. Da Fig. 3.2 vemos que o raio (1) incidente sobre a lente é descrito pela altura Y_i⁽¹⁾ = d’ e pelo ângulo q_i⁽¹⁾ = arctg d’/f d’/f, enquanto que o raio emergente é caracterizado por Y_e⁽¹⁾= d’ e q_e⁽¹⁾ = 0. Logo, poderemos montar a seguinte equação matricial:

(3.3)

que nos leva ao sistema de equações:

Para o raio (2), temos Y_i⁽²⁾ = -d, q_i⁽²⁾ = 0, Y_e⁽²⁾ = -d e q_e⁽²⁾ = arctg d/f d/f. Portanto,

(3.5)

de onde se obtém:

Substituindo estes valores na eq. (3.4) encontramos S₁₂ = 0 e S₂₂ = 1, de forma que a matriz da lente positiva fica:

(3.7)

Para uma lente negativa (divergente) basta que se troque o sinal de f, como será demonstrado no problema 3.3. A determinação das matrizes de vários sistemas ópticos e suas combinações será deixada para a seção de exercícios. O procedimento a ser adotado na solução destes problemas é análogo ao que usamos para a lente positiva. Um fato que merece destaque é que as matrizes que representam os elementos ópticos, a exemplo da matriz da lente convergente, são unitárias. Logo, quando temos um sistema óptico composto de vários elementos, sua matriz também é unitária, pois é a resultante de um produto de matrizes unitárias. A seguir, vamos introduzir alguns conceitos envolvendo lentes finas e espessas.

Sergio Carlos Zilio