|

Quando v�rias lentes finas s�o colocadas bem pr�ximas (em contato), a
dist�ncia focal combinada do conjunto pode ser expressa como:
onde fi é a distância focal da i-ésima lente. Esta
equação é facilmente obtida multiplicando-se
as matrizes das lentes, que deduzimos no final da seção
anterior.
Por outro lado, no caso em que duas lentes finas, de distâncias
focais f1 e f2, estão separadas de uma distância d, como
mostrado na Fig. 3.6, a matriz que descreve o conjunto é:
onde o foco efetivo é dado por:
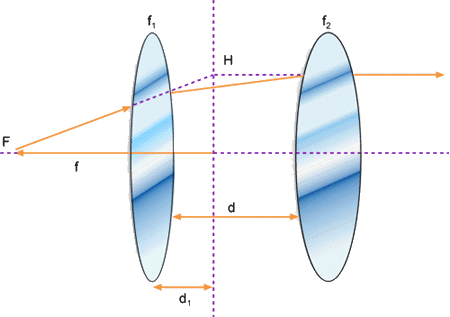
Fig. 3.6 - Associação de duas lentes separadas por
uma distância d.
O
traçado dos raios está descrito no texto.
Para entendermos um pouco melhor como funciona este sistema, vamos
considerar um raio de luz que sai do foco efetivo, F, atravessa o
conjunto e se torna paralelo ao eixo óptico como mostra a Fig.
3.6a. Se traçarmos os prolongamentos dos raios que sai de F
e aquele paralelo ao eixo, eles se interceptarão sobre um plano
(H), chamado de plano principal. Qualquer outro raio saindo do foco
com ângulo diferente daquele mostrado, produzirá uma
intersecção com o correspondente raio paralelo ao eixo
óptico em algum ponto do plano H. Para efeitos práticos,
é como se houvesse uma lente de distância focal f localizada
em H.
O raio que chega à lente f1
é caracterizado por uma altura Yi
e por um ângulo qi = Yi /(f-d1), onde d1 é
a distância do plano principal à lente f1. O raio que sai da lente f2é caracterizado pelos parâmetros Ye
= Yi +
d1qi e qe = 0. Usando o formalismo matricial, onde a matriz Mc dada em (3.18) é aplicada ao raio incidente, temos:
de onde obtemos a distância do plano primário à
lente f1:
Procedendo da mesma forma para o raio mostrado na Fig. 3.6b, encontramos
que a distância do plano secundário (H’) à
lente f2é dada por:
A eq.(3.8) de formação de imagens continua válida,
mas s é a distância entre o objeto e o plano primário
e s’ entre a imagem e o plano secundário.
Sergio Carlos Zilio
|