|
Embora Hamilton tivesse desenvolvido a analogia exposta na seção
precedente ainda em 1828, ele não tinha motivos para atribuir
qualquer caráter ondulatório a uma dada partícula.
Desta forma, por falta de evidências experimentais não
foi possível a ele encontrar uma equação de ondas
para descrever o comportamento da partícula. Foi Erwin Schrödinger
que, em 1927, estendeu a analogia de Hamilton e encontrou uma equação
de ondas para descrever o movimento de um ponto material. A idéia
seguida por Schrödinger está esquematizada na Fig. 2.10.
Sabia-se que a óptica geométrica era um caso limite
da óptica ondulatória e que era análoga à
mecânica Newtoniana de uma partícula. Seria possível
obter alguma equação, no mesmo pé de igualdade
da equação de ondas eletromagnéticas, que levaria
à mecânica clássica no limite em que alguma grandeza,
, inerente à esta teoria tendesse a zero?
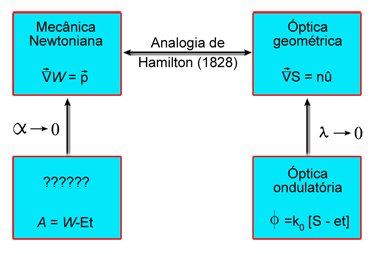
Fig. 2.10 - Conjectura de Schrödinger.
Da analogia de
Hamilton, W corresponde ao eikonal S. Levando-se em conta a parte
temporal, a ação A = W -Et deve corresponder à
fase da onda eletromagnética, dada por:
onde as substituições k0 = 2p/l0
e l0 = c/n foram introduzidas. Comparando
os termos com dependência temporal na fase da onda e na ação,
Schrödinger concluiu que a energia da partícula deveria
ser proporcional à frequência de alguma onda associada
a ela, cuja propagação está mostrada na Fig.
2.9. Assim,
onde h é uma constante de proporcionalidade, que mais tarde foi
identificada como sendo a constante de Planck. Associando um comprimento
de onda à propagação da superfície A(t)
no espaço das configurações e levando em conta
que esta se propaga com uma velocidade de fase dada por vf
= E/p, temos:
Desta forma, Schrödinger conseguiu associar um comprimento de onda
à partícula de momentum p. Este comprimento de onda
foi posteriormente deduzido por de Broglie de uma outra maneira e
porisso leva o nome de comprimento de onda de de Broglie. A eq. (2.65)
permite encontrar o vetor de propagação como:
onde
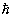 = h/2p
, e as relações p2
= 2mT e E = T-V foram utilizadas. Substituindo o valor de k dado em (2.66)
na equação de ondas reduzida, eq. (2.37), chegamos à
equação de Schrödinger: = h/2p
, e as relações p2
= 2mT e E = T-V foram utilizadas. Substituindo o valor de k dado em (2.66)
na equação de ondas reduzida, eq. (2.37), chegamos à
equação de Schrödinger:
onde o vetor campo elétrico foi substituido por uma nova função,
y, cuja interpretação será deixada para
os textos de mecânica quântica.
Em resumo, para se obter a equação de Schrödinger,
é necessário associar um comprimento de onda à
partícula de momentum p (comprimento de onda de de Broglie)
e isto pode ser feito estendendo-se a analogia de Hamilton. A partir
disto, usa-se a conservação de energia e a equação
de ondas na sua forma reduzida para a obtenção da equação
de Schrödinger.
Para finalizarmos esta seção, vamos mostrar que a velocidade
de grupo associada à propagação da superfície
de ação constante corresponde à velocidade da
partícula. Como veremos no Cap. V, a velocidade de grupo, ou
de pacote de onda, é dada por:
com w = 2pn . Usando a eq. (2.65), e considerando que
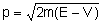 e E = hn
, temos: e E = hn
, temos:
cuja derivada com respeito a nos fornece vg-1:
Substituindo hn por E e
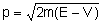 , obtemos vg = p/m = v. , obtemos vg = p/m = v.
Sergio Carlos Zilio
|