|
O Potencial Ótico
Como vimos na seção anterior, as equações
de ondas eletromagnéticas e de Schrödinger são
formalmente equivalentes desde que se associe o comprimento de onda
de de Broglie à partícula. No limite clássico
da equação de Schrödinger, que corresponde ao caso
h 0 ( 0), recuperamos as equações da mecânica
clássica. Para sistemas conservativos temos:
e este tipo de equação também deve existir na óptica
geométrica devido à equivalência entre as duas
equações de ondas. Usando (2.66), podemos definir um
potencial óptico como:
Na presente analogia, a óptica geométrica está
ligada ao limite clássico da equação de Schrödinger,
no qual a 2a lei de Newton é válida. Desta forma,
Como k(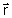 ) = k0n( ) = k0n(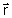 ) e k0 = w/c, temos: ) e k0 = w/c, temos:
Assim, obtemos a aceleração que atua sobre uma partícula
de luz quando esta atravessa um meio com índice de refração
variável. Entretanto, a eq. (2.74) mistura o caráter
de uma partícula de massa m com o de onda (w,c).
Para eliminarmos a massa desta equação, faremos uso
da relação de de Broglie:
onde k0 = w/v = nw/c.
Substituindo (2.74) em (2.73) obtemos uma expressão para a
aceleração de um raio de luz que se propaga com velocidade
v = c/n num meio cujo índice de
refração depende da posição:
Entretanto, a solução desta equação é
complicada, uma vez que v também pode depender da posição.
Para simplificá-la, vamos tomar a aproximação
paraxial que estabelece que o movimento do raio está confinado
em torno do eixo de propagação, que denominaremos de
z. Neste caso, v 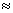 dz/dt e a aceleração pode ser expressa como:
dz/dt e a aceleração pode ser expressa como:
onde a regra da
cadeia foi utilizada. Substituindo (2.77) em (2.76) e cancelando v
obtemos:
Usando
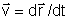 e aplicando novamente a regra da cadeia chegamos a:
e aplicando novamente a regra da cadeia chegamos a:
que nos leva à equação de propagação
de raios:
Podemos comparar este resultado com a equação dos raios
obtida anteriormente. Usando a aproximação paraxial
(d/ds
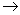 d/dz) na eq. (2.31) e realizando a primeira derivada com respeito
a z, temos: d/dz) na eq. (2.31) e realizando a primeira derivada com respeito
a z, temos:
Vemos então que o primeiro termo desta equação
não aparece em (2.80). Para efeitos práticos isto não
tem muita importância, pois a duas equações são
válidas apenas na aproximação paraxial, que só
tem sentido quando a variação de n é muito pequena.
Na solução da eq. (2.81), despreza-se em geral o primeiro
termo e aproxima-se n por n0 no segundo
termo.
Podemos entender a ausência do termo proporcional a dn/dz em
(2.80) re-escrevendo o potencial óptico como:
que corresponde a um termo constante e outro muito pequeno. Para passarmos
do caso quântico para o clássico devemos ter h 0. Isto
significa que os níveis de energia do sistema são quase
contínuos e para isto o potencial deve variar lentamente no
espaço. Assim, o primeiro termo de (2.81) pode ser considerado
como de 2a ordem e portanto desprezado.
Em conclusão, introduzimos um potencial óptico com o
qual obtivemos uma equação que descreve a propagação
dos raios na aproximação paraxial. Este conceito é
interessante porque através dele podemos entender porque os
raios de luz procuram sempre as regiões de maior índice
de refração (menor potencial). Como exemplo, numa fibra
óptica o núcleo possui índice de refração
levemente superior ao da casca, o que garante que os raios de luz
fiquem confinados próximos ao seu centro.
Sergio Carlos Zilio
|