|

Em 1828, Hamilton formulou a analogia entre a óptica geométrica
e a mecânica Newtoniana de uma partícula. Esta formulação
está discutida em detalhes na referência 2.3 e aqui fazemos
apenas um breve resumo das idéias envolvidas. Já vimos
um pouco desta analogia quando estudamos o princípio de Fermat,
que é equivalente ao princípio da mínima ação,
ou ação estacionária. Vamos ver agora outros
aspectos desta equivalência. Para a obtenção da
equação de Hamilton-Jacobi, lembremo-nos que a ação
é dada por:
onde L é a Lagrangeana, q e p são respectivamente a coordenada
e velocidade generalizadas, t é o tempo e C é uma constante.
Denominando de H o Hamiltoniano do sistema mecânico e fazendo
uma transformação canônica tal que o novo Hamiltoniano,
K, seja nulo, obtemos a equação de Hamilton-Jacobi:
No caso em que a energia se conserva, H não depende do tempo
e a eq. (2.52) pode ser integrada, resultando em:
onde H = E é a energia da partícula,
A é a função principal de Hamilton e W é
conhecida como função característica de Hamilton.
Na eq. (2.52), o momentum é representado por
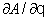 , e como nos sistemas conservativos apenas W depende de q, como
visto na eq. (2.53), temos , e como nos sistemas conservativos apenas W depende de q, como
visto na eq. (2.53), temos
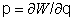 . Este resultado pode ser estendido para três dimensões
fornecendo: . Este resultado pode ser estendido para três dimensões
fornecendo:
Isto significa que a partícula caminha perpendicularmente à
superfície definida pela função W. Neste ponto
já é possível notar-se alguma semelhança
com a óptica geométrica, pois de acordo com a eq. (2.41),
um raio de luz propaga-se perpendicularmente à superfície
S(x,y,z), com o índice de refração fazendo o
papel de momentum.
Para analisarmos o movimento de uma partícula, consideremos
a superfície A = constante = a, como uma frente de onda propagando-se no espaço
das configurações. De acordo com a Fig. 2.9, a variação
da função W num intervalo de tempo dt é dada
por:
Usando o conceito de derivada direcional temos:
onde 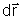 é um vetor perpendicular à superfície A
= constante. Igualando as equações (2.55) e (2.56) obtemos
a velocidade de fase para a propagação da frente de
onda como: é um vetor perpendicular à superfície A
= constante. Igualando as equações (2.55) e (2.56) obtemos
a velocidade de fase para a propagação da frente de
onda como:
onde T=p2/2m é a energia cinética da partícula.
Deste modo, vemos que a velocidade de fase aumenta quando a velocidade
da partícula diminui. Entretanto, como veremos posteriormente,
é a velocidade de grupo (velocidade de um pacote de onda) que
é igual à velocidade da partícula, e não
a velocidade de fase.
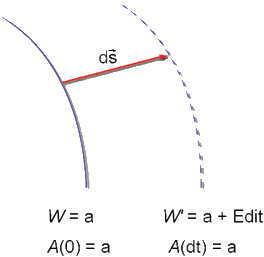
Fig. 2.9 - Propagação da superfície A(t)=a no
espaço das configurações.
Para realizarmos uma comparação formal entre a óptica
geométrica e a mecânica clássica, vamos inicialmente
mostrar que a equação do eikonal tem sua origem na óptica
ondulatória no limite em que 0. Para isto não podemos
usar a equação de ondas na forma reduzida, dada pela
eq. (2.37), mas sim sua forma completa, que envolve a derivada temporal.
Esta equação, que será deduzida no Cap. 4, é
dada por:
onde o aspecto
vetorial do campo elétrico foi ignorado para simplificar as
contas. A solução desta equação é
obtida generalizando-se a eq. (2.38) de acordo com:
onde a amplitude do campo elétrico foi escrita como 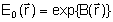 por conveniência. A substituição de (2.59)
em (2.58), que será deixada como exercício, nos leva
a: por conveniência. A substituição de (2.59)
em (2.58), que será deixada como exercício, nos leva
a:
Como as grandezas B e S são reais, cada termo entre colchetes
deve se anular separadamente. Assim temos:
No limite em que l
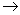 0 (k0 0 (k0
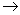 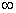 ), apenas os dois últimos termos de (2.61b) são
relevantes, o que nos leva à equação do eikonal
já discutida anteriormente. ), apenas os dois últimos termos de (2.61b) são
relevantes, o que nos leva à equação do eikonal
já discutida anteriormente.
Em resumo, a solução da equação de ondas
eletromagnéticas possui uma fase que é dada por:
e no limite em que l
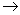 0 obtemos que o raio de luz se propaga com uma direção
definida por 0 obtemos que o raio de luz se propaga com uma direção
definida por
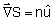 . Já na mecânica clássica, a direção
de propagação de uma partícula é dada
pela eq. (2.54). Assim, a função característica
W(q,p) faz o papel de eikonal e . Já na mecânica clássica, a direção
de propagação de uma partícula é dada
pela eq. (2.54). Assim, a função característica
W(q,p) faz o papel de eikonal e
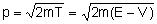 (onde V representa a energia potencial), faz o papel de índice
de refração. A análise da equação
de Hamilton-Jacobi indica que a mecânica clássica é
análoga ao limite da óptica geométrica da equação
de ondas. Raios de luz ortogonais às frentes de onda (equifases)
correspondem à trajetórias de partículas, ortogonais
as superfícies de ação constante. Na seção
seguinte, vamos ver como Schrödinger estendeu a analogia de Hamilton
para obter uma equação básica na mecânica
quântica, que hoje leva seu nome. (onde V representa a energia potencial), faz o papel de índice
de refração. A análise da equação
de Hamilton-Jacobi indica que a mecânica clássica é
análoga ao limite da óptica geométrica da equação
de ondas. Raios de luz ortogonais às frentes de onda (equifases)
correspondem à trajetórias de partículas, ortogonais
as superfícies de ação constante. Na seção
seguinte, vamos ver como Schrödinger estendeu a analogia de Hamilton
para obter uma equação básica na mecânica
quântica, que hoje leva seu nome.
Sergio Carlos Zilio
|