|

Neste ponto, deixaremos de lado a óptica geométrica para
introduzirmos o conceito de eikonal. Esta função, obtida
a partir da óptica ondulatória, é importante
pois representa o papel da função característica
de Hamilton na mecânica clássica e é de grande
valia quando se faz a analogia desta com a óptica geométrica.
Como veremos no Cap. IV, a equação das ondas eletromagnéticas
na sua forma reduzida (sem dependência temporal) é dada
por:
onde k(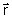 ) = 2pn( ) = 2pn(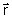 )/l é o é vetor de propagação,
que depende da posição, uma vez que n( )/l é o é vetor de propagação,
que depende da posição, uma vez que n(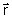 ) depende da posição num meio não homogêneo.
A solução da equação de ondas é
uma grandeza complexa, que contém um termo de amplitude e outro
de fase, e pode ser escrita como: ) depende da posição num meio não homogêneo.
A solução da equação de ondas é
uma grandeza complexa, que contém um termo de amplitude e outro
de fase, e pode ser escrita como:
sendo E0(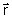 ) a amplitude (envelope), f() a fase da onda e S( ) a amplitude (envelope), f() a fase da onda e S(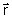 ) a função eikonal, que dá a direção
de propagação da onda em termo de seus co-senos diretores.
k0 é o vetor de onda no vácuo, dado por k0=2pn/l , onde l é o comprimento de onda da luz no vácuo
(n=1).
As superfícies S( ) a função eikonal, que dá a direção
de propagação da onda em termo de seus co-senos diretores.
k0 é o vetor de onda no vácuo, dado por k0=2pn/l , onde l é o comprimento de onda da luz no vácuo
(n=1).
As superfícies S(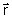 ) = constante
formam as equifases da onda, e esta se propaga perpendicularmente
a estas superfícies. Para visualizarmos este fato, consideremos
uma onda plana, cuja fase é dada por: ) = constante
formam as equifases da onda, e esta se propaga perpendicularmente
a estas superfícies. Para visualizarmos este fato, consideremos
uma onda plana, cuja fase é dada por:
como veremos posteriormente.
Assim, a função eikonal fica sendo:
A direção perpendicular a esta superfície pode
ser encontrada pelo cálculo de seu gradiente:
onde û é um versor paralelo a
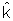 e que portanto define a direção de propagação
da onda. Realizando o produto escalar e que portanto define a direção de propagação
da onda. Realizando o produto escalar
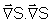 obtemos: obtemos:
que é conhecida como a equação do eikonal. Esta
equação também pode ser obtida diretamente pela
substituição da eq. (2.38) em (2.37), mas isto será
deixado como exercício.
O conceito de função eikonal pode ser utilizado na dedução
da equação dos raios que obtivemos na seção
2.6. Fazendo uso da Fig. 2.6, de onde temos |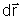 |=ds e û= |=ds e û=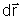 /ds,
podemos escrever /ds,
podemos escrever
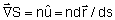 , sendo que este último termo já é o que
entra na equação dos raios. Tendo em mente a eq. (2.31)
escrevemos: , sendo que este último termo já é o que
entra na equação dos raios. Tendo em mente a eq. (2.31)
escrevemos:
O lado direito da equação pode ser trabalhado com o uso
da regra da cadeia:
e pelo cálculo do gradiente da eq. (2.42) (equação
do eikonal):
Usando
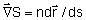 no segundo termo desta equação obtemos: no segundo termo desta equação obtemos:
onde a eq. (2.44) foi utilizada no primeiro termo da esquerda. Substituindo
a igualdade da direita na eq. (2.43) recuperamos a equação
dos raios.
Com a função eikonal é possível obter-se
as condições de contorno para os raios de luz. Lembrando
que o rotacional do gradiente é nulo, temos:
onde o teorema de Stokes foi usado. Como
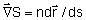 , temos: , temos:
Nesta última passagem supusemos que o caminho de integração
coincide com o caminho dos raios de luz, isto é, û é
paralelo a
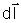 . De acordo com a Fig. 2.7 podemos definir os caminhos C1
e C2, e a eq. (2.48) pode ser expressa
como: . De acordo com a Fig. 2.7 podemos definir os caminhos C1
e C2, e a eq. (2.48) pode ser expressa
como:
de onde concluimos que dois raios de luz que deixam um ponto P1
e chegam até um ponto P2 por
caminhos geométricos diferentes, o fazem com o mesmo valor
de caminho óptico. Exemplificando, todos os raios que saem
de um dado ponto de um objeto colocado na frente de uma lente e chegam
ao mesmo ponto da imagem, o fazem de tal forma que as integrais de
linha de nds por diferentes caminhos geométricos fornecem o
mesmo valor.
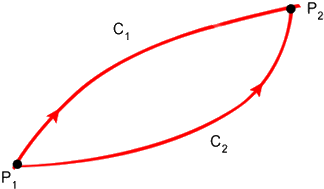
Fig. 2.7 - Possíveis caminhos seguidos pelos raios de luz.
Podemos também usar a eq. (2.48) para deduzir a lei de Snell.
Neste caso, o caminho de integração dado pela curva
C não corresponde à direção de propagação
dos raios de luz. Considere a Fig. 2.8, que mostra raios incidentes
sobre uma interface que separa dois meios. Neste caso temos:
que nos leva diretamente à lei de Snell, já que û.ê
= senq. A seguir, vamos usar a idéia de função
eikonal para estabelecer um paralelo entre a óptica geométrica
e a mecânica clássica.
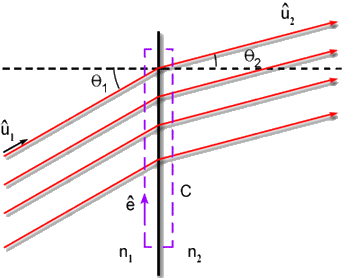
Fig 2.8 - Raios de luz que incidem numa interface dielétrica.
Sergio Carlos Zilio
|