|

Através da manipulação matemática das equações
de Euler-Lagrange, obtidas com o princípio de Fermat, é
possível a obtenção de uma equação
vetorial elegante, que descreve a propagação de um raio
num meio óptico não homogêneo. Para deduzirmos
esta equação dos raios, começaremos com a eq.
(2.20a):
onde a expressão para f, dada pela eq. (2.18), foi utilizada
na derivada relativa a x. Efetuando também a derivada com relação
a obtemos:
Da eq. (2.16) temos:
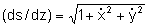 . Portanto, usando a regra da cadeia no termo . Portanto, usando a regra da cadeia no termo
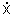 =dx/dz do lado esquerdo da equação temos: =dx/dz do lado esquerdo da equação temos:
Aplicando novamente a regra da cadeia na derivada relativa a z chegamos
a:
Partindo da outra equação de Euler-Lagrange, eq. (2.20b),
obtemos de forma análoga a expressão envolvendo a coordenada
y:
Combinando as equações (2.28) e (2.29) é possível
encontrar uma expressão análoga para a coordenada z:
Multiplicando as equações (2.28), (2.29) e (2.30) respectivamente
pelos versores î,
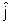 e e
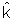 , e somando as três, obtemos a equação vetorial
que fornece a propagação do raio dentro do meio não
homogêneo: , e somando as três, obtemos a equação vetorial
que fornece a propagação do raio dentro do meio não
homogêneo:
A Fig. 2.6 mostra a geometria de s, ds,
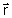 e e
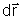 . É interessante notar que | . É interessante notar que |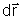 | = ds. A direção
de propagação do raio de luz é caracterizada
por um versor û = | = ds. A direção
de propagação do raio de luz é caracterizada
por um versor û =
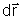 /ds. O vetor é definido a partir da escolha de uma origem
arbitrária, s é o deslocamento ao longo do raio e ds
é um incremento infinitesimal deste deslocamento. /ds. O vetor é definido a partir da escolha de uma origem
arbitrária, s é o deslocamento ao longo do raio e ds
é um incremento infinitesimal deste deslocamento.
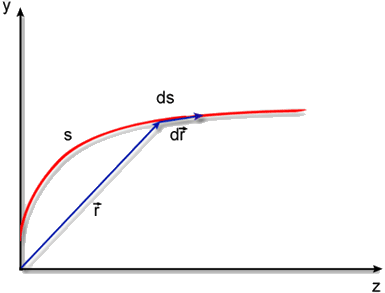
Fig. 2.6 - Geometria das grandezas utilizadas na equação
dos raios.
Para finalizarmos esta seção, vamos aplicar a equação
dos raios à análise da propagação de luz
pela mistura de água e álcool. O uso da eq. (2.31) é
em geral simples na aproximação paraxial, onde o desvio
do raio é pequeno. Neste caso, ds está praticamente
na direção z e assim podemos substituir d/ds por d/dz.
Como a trajetória do raio se dá no plano yz, escrevemos
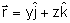 , de onde tiramos , de onde tiramos
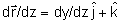 . O gradiente de n pode ser calculado a partir da eq. (2.1) e
resulta em . O gradiente de n pode ser calculado a partir da eq. (2.1) e
resulta em
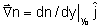 . Substituindo estas grandezas na equação dos raios
obtemos: . Substituindo estas grandezas na equação dos raios
obtemos:
Como n(y) não depende de z, ele pode ser tirado para fora da
derivada. é um vetor constante e sua derivada relativa a z
é nula. Portanto, da equação vetorial (2.32)
sobra apenas a componente na direção , dada por:
onde n(y), dado pela eq. (2.1) já foi substituido.
Na aproximação paraxial, o raio se desvia pouco do eixo
z (y
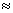 y0) e além disto dn/dy
é pequeno. Logo podemos desprezar o segundo termo entre colchetes
do lado esquerdo da equação e assim obtemos uma expressão
onde a derivada segunda de y é constante (equação
da parábola). A solução desta equação
é simples e leva aos resultados já obtidos anteriormente: y0) e além disto dn/dy
é pequeno. Logo podemos desprezar o segundo termo entre colchetes
do lado esquerdo da equação e assim obtemos uma expressão
onde a derivada segunda de y é constante (equação
da parábola). A solução desta equação
é simples e leva aos resultados já obtidos anteriormente:
que
implica em:
de
forma que
onde as condições iniciais
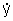 (z=0)=0
e y(z=0)=y0 foram utilizadas. Portanto, recuperamos os resultados
já encontrados pela lei de Snell generalizada e pelas equações
de Euler-Lagrange. (z=0)=0
e y(z=0)=y0 foram utilizadas. Portanto, recuperamos os resultados
já encontrados pela lei de Snell generalizada e pelas equações
de Euler-Lagrange.
Sergio Carlos Zilio
|