|

Introduzido em 1657, o princípio de Fermat estabelece que a luz se
propaga entre dois pontos no menor tempo possível, no caso em que ela
não sofre reflexões. Consideremos um raio se propagando por meios com
diferentes índices de refração, conforme mostra a Fig. 2.4. O tempo
total para ele realizar o percurso indicado é dado pela somatória dos
tempos gastos em cada meio:
onde di é a distância percorrida em cada meio, com velocidade
vi = c/ni.
c é a velocidade da luz no vácuo e nié
o índice de refração do i-ésimo meio.
A somatória [
 ] = ] =
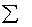 nidi
é denominada de caminho óptico. Como c é constante,
o tempo mínimo implica no menor caminho óptico possível. nidi
é denominada de caminho óptico. Como c é constante,
o tempo mínimo implica no menor caminho óptico possível.
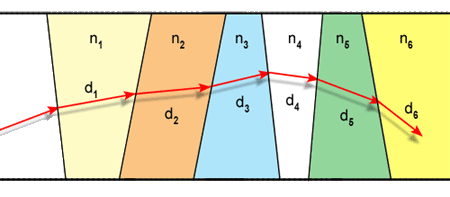
Fig. 2.4 - Raio se propagando numa série de meios homogêneos
com índices de refração diferentes.
| Uma aplicação simples do princípio de Fermat é
a dedução da lei de Snell, que apresentamos
a seguir. Consideremos um raio que se propaga entre dois pontos
fixos, P1 e P2, localizados em
meios com índices de refração distintos,
n1 e n2, conforme mostra a Fig. 2.5. As distâncias x1
e x2 são fixas, mas y1
e y2 podem variar para a
minimização do tempo. Entretanto, como os pontos
P1 e P2
são fixos, y1+y2 = Y é constante. O
caminho óptico será dado por: |
|
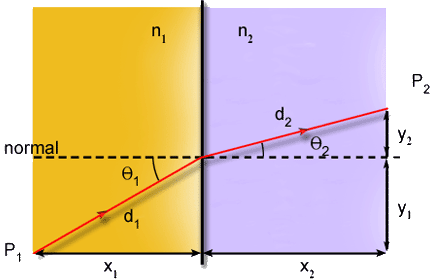
Fig. 2.5 - Geometria utilizada na dedução da lei de
Snell pelo princípio de Fermat.
que de acordo com a geometria da Fig. 2.5 pode ser expresso como:
A eq. (2.11) estabelece a variação de [ D
] com y1. Para encontrarmos seu valor
mínimo igualamos sua derivada a zero:
De acordo com a geometria da Fig. 2.5, as frações da eq.
(2.12) correspondem aos senos de 1 e 2, de forma que assim obtemos
a lei de Snell:
Até agora nossa apresentação do princípio
de Fermat restringiu-se ao caso em que a luz se propaga através
de vários meios homogêneos, porém com diferentes
índices de refração. Queremos agora analisar
o caso em que a propagação ocorre num meio em que o
índice de refração varia continuamente ao longo
do percurso do raio. Neste caso, a somatória da eq. (2.9) deve
naturalmente ser substituída por uma integral:
onde s é distância percorrida pelo feixe entre os pontos
P1 e P2 e n(s)ds é o caminho óptico elementar.
O princípio de Fermat estabelece a existência de um caminho
muito bem definido para o raio ir de P1
e P2. Trata-se de um princípio
variacional que pode ser colocado da seguinte maneira:
Quando um raio se propaga no espaço, ds é expresso em
coordenadas cartesianas como:
onde
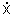 = dx/dz e = dx/dz e
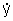 = dy/dz. Note que dz foi arbitrariamente
colocado em evidência, mas também poderíamos ter
escolhido dx ou dy. Assim, o princípio de Fermat fica: = dy/dz. Note que dz foi arbitrariamente
colocado em evidência, mas também poderíamos ter
escolhido dx ou dy. Assim, o princípio de Fermat fica:
com:
onde supusemos que n pode variar nas três direções.
A solução da eq. (2.17) já foi estabelecida no
contexto da mecânica clássica, explicitamente ao se tratar
o princípio da mínima ação:
onde L (x,y,z,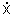 , ,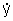 ,z) é a Lagrangeana do sistema mecânico, x, y, e
z são as coordenadas cartesianas e t é o tempo. Comparando
as equações (2.17) e (2.19), notamos que f(x,y,z, ,z) é a Lagrangeana do sistema mecânico, x, y, e
z são as coordenadas cartesianas e t é o tempo. Comparando
as equações (2.17) e (2.19), notamos que f(x,y,z,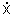 , ,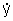 ,z) faz o papel da Lagrangeana e z, o de tempo. Como já
estudado na mecânica clássica, a solução
da eq. (2.17) leva a um conjunto de equações do tipo
Euler-Lagrange: ,z) faz o papel da Lagrangeana e z, o de tempo. Como já
estudado na mecânica clássica, a solução
da eq. (2.17) leva a um conjunto de equações do tipo
Euler-Lagrange:
Queremos agora aplicar estas equações na análise
da trajetória do raio se propagando na mistura de água
e álcool. De acordo com a simetria do problema, a trajetória
do raio está confinada no plano yz e a função
f independe de x e
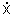 . Em geral, a análise de problemas onde o índice
de refração depende de apenas uma coordenada torna-se
matematicamente mais simples se a coordenada "tempo" for tomada na
direção em que n varia. Assim, tomaremos . Em geral, a análise de problemas onde o índice
de refração depende de apenas uma coordenada torna-se
matematicamente mais simples se a coordenada "tempo" for tomada na
direção em que n varia. Assim, tomaremos
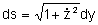 , onde agora dy foi colocado em evidência. Neste caso, a
equação de Euler-Lagrange torna-se: , onde agora dy foi colocado em evidência. Neste caso, a
equação de Euler-Lagrange torna-se:
onde
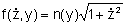 independe de z e portanto independe de z e portanto
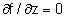 . Isto simplifica a solução da eq. (2.21) pois . Isto simplifica a solução da eq. (2.21) pois
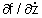 será constante. Desta forma, temos: será constante. Desta forma, temos:
onde a condição inicial b(y0)=0 foi usada. Note que tg b(y0)=dy/dz=0 para z=0
(y=y0). Portanto, 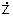 = cotg = = cotg =
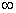 neste ponto e os neste ponto e os
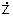 do numerador e denominador da eq. (2.22) se cancelam. Elevando
esta equação ao quadrado obtemos: do numerador e denominador da eq. (2.22) se cancelam. Elevando
esta equação ao quadrado obtemos:
Substituindo a expressão aproximada para o índice de refração
n(y) 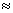 n0 + (dn/dy)(y-y0) e considerando que n0 + (dn/dy)(y-y0) e considerando que
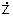 = dz/dy =1/(dy/dz) =1/ = dz/dy =1/(dy/dz) =1/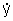 , obtemos: , obtemos:
onde o termo quadrático em dn/dy foi desprezado. Esta equação
é idêntica à eq. (2.5) e sua integração
leva à trajetória parabólica da eq. (2.6) obtida
na seção precedente. Com esta análise chegamos
ao mesmo resultado obtido com a lei de Snell generalizada. Entretanto
convém salientarmos que as equações de Euler-Lagrange
são mais gerais pois permitem tratar problemas onde o índice
de refração varia nas três direções.
Sergio Carlos Zilio
|