Como se tornará evidente mais adiante, este tipo de abordagem se aplica ao caso unidimensional, ou seja, quando o índice de refração varia em apenas uma direção. Como exemplo desta situação, tomemos uma mistura não homogênea de água (n=1.333) e álcool (n=1.361), que apresenta uma variação de índice de refração como indicada na Fig. 2.2.

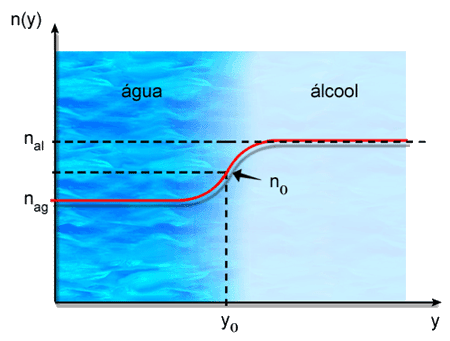
Fig. 2.2 - Variação do índice de refração numa mistura não homogênea de água e álcool (nág=1.333 e nal=1.361).

Vamos ainda supor que o raio de luz penetra nesta mistura a uma altura y₀, localizada na região de transição água-álcool, propagando-se ao longo do eixo z. Esta situação está esquematizada na Fig. 2.3. Como a variação de n é pequena e ocorre numa região relativamente grande (da ordem de um centímetro), admitiremos que o desvio sofrido pelo feixe é pequeno. Assim, o raio deslocar-se-á pouco da altura y0 e o índice de refração pode ser expandido em série de Taylor, de acordo com:

(2.1)

onde n₀ e dn/dy]_y0 são respectivamente o índice de refração e seu gradiente na altura y₀. A seguir, vamos utilizar a lei de Snell, que já era conhecida experimentalmente em 1621. Para isto, vamos imaginar a região de transição água-álcool dividida num grande número de lâminas planas e paralelas, de espessuras tão finas quanto se queira, de forma que em cada uma delas o índice de refração é praticamente constante. As lâminas são paralelas ao eixo z e portanto perpendiculares à direção em que n varia. O paralelismo entre as faces de cada lâmina é motivado pelo fato de n variar apenas ao longo de y.

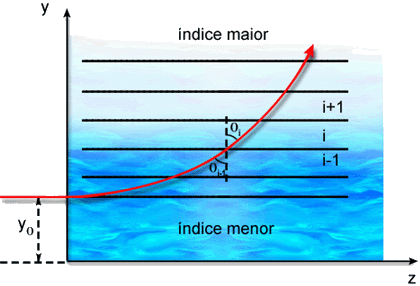
Fig. 2.3 - Desvio de um raio de luz que incide na mistura água-álcool a uma altura y₀. A magnitude do desvio foi exagerada para melhor visualização.

Podemos aplicar a lei de Snell na interface que separa duas lâminas consecutivas i e i-1: n_i-1 sen q_i-1= n_i sen q_i, onde q_i é o ângulo que o raio faz com o eixo y. Como o índice de refração é constante em cada uma das lâminas, o raio se propaga em linha reta até a próxima interface, onde chega com o ângulo de incidência i. Novamente aplicamos a lei de Snell: n_i sen q_i = n_i+1 sen q_i+1. Desta forma, o produto n sen mantém-se constante conforme o raio se propaga pelas diferentes lâminas. Tomando o limite em que as espessuras das lâminas tendem a zero, obtemos a lei de Snell generalizada:

que estabelece que o ângulo q varia continuamente com y, conforme n varia. Podemos ainda trabalhar com o ângulo b(y) que o raio faz com as faces das lâminas. Levando em conta que b é o ângulo complementar de q e que o raio inicialmente propaga-se ao longo do eixo z (b(y₀)= 0), a lei de Snell generalizada fica:

O raio descreve uma trajetória curva dada por y = y(z), cuja inclinação é:

(2.4)

Usando as expressões de cos b e n(y) dadas pelas equações (2.3) e (2.1), temos:

(2.5)

onde o termo quadrático em dn/dy foi desprezado. A eq. (2.5) pode facilmente ser integrada resultando em:

(2.6)

que representa a trajetória parabólica do raio dentro do meio. No capítulo final do livro apresentamos uma demonstração na qual se mede o desvio de um raio de luz laser ao percorrer uma certa distância dentro do meio. Isto possibilita a medida do gradiente do índice de refração como função da altura y. Devido ao fato deste gradiente não ser constante, observamos a focalização (ou desfocalização) da luz do laser, como descrito a seguir.

Consideremos um feixe de luz laser com diâmetro y, de tal forma que a parte inferior do raio penetra no meio a uma altura y₀ e a parte superior em y₀ + y. Vamos ainda considerar y suficientemente pequeno tal que o índice de refração seja aproximadamente o mesmo (n₀) ao longo de todo o perfil transversal do feixe. A uma distância z no interior do meio, a parte inferior do feixe satisfará a eq. (2.6), enquanto que a parte superior executará uma trajetória descrita por:

(2.7)

e assim, o diâmetro do feixe, F = y'-y, como função da distância de propagação, fica:

(2.8)

Desta forma, o desvio sofrido pelo feixe está ligado ao gradiente de n, enquanto que seu diâmetro fornece a derivada segunda de n. De acordo com a Fig. 2.2, próximo da água o feixe será desfocalizado e na região mais próxima do álcool haverá focalização. Voltaremos a discutir este assunto quando apresentarmos a demonstração do capítulo final.

Sergio Carlos Zilio