|
Utilizando a identidade
vetorial
,
a expressão
transforma-se
em
Para as componentes
no sistema solidário do corpo rígido, temos
.
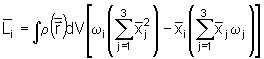A i-ésima
componente pode ser escrita como
,
onde
são as
componentes do tensor de inércia.
Utilizando uma
notação mais compacta temos
,
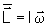
onde I é
o tensor de inércia escrito de uma forma matricial
.
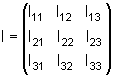
Observe-se
que sob uma rotação do sistema de eixos solidário
ao corpo rígido, as coordenadas sofrem a transformação
.
Espera-se
pois que sob uma rotação o tensor Iij
também se transforme:
.
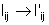Para determinarmos como o tensor Iij
se transforma sob uma rotação, lembremo-nos
de que as coordenadas se transformam de acordo com
.
|
|
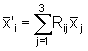A partir da equação
anterior podemos verificar facilmente que após a rotação
o tensor Iij se transforma da seguinte maneira
.
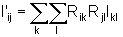
Em notação
matricial dizemos que o tensor I se transforma como
,
onde
.
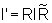
Uma transformação
dada pela equação anterior e
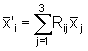é conhecida por transformação de semelhança
e onde sabemos que, no caso de rotação,
 .
|
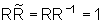