|
O
momento angular, L, é uma grandeza física muito importante,
especialmente em se tratando de rotações, mas cuja definição
é um tanto quanto abstrata. Ela é definida como o produto
vetorial do vetor posição e do vetor quantidade de movimento.
L
= r x p
Vê-se
que L é um vetor perpendicular a r e a p e, por isso, na maioria
das vezes, ela acaba levando a dificuldades de visualização.
No entanto, é uma quantidade física fundamental e importante
no estudo da rotação de um corpo.
A
quantidade de movimento de um corpo pode ser nula (o que significa
que ele nã está em movimento de translação)
e ainda assim ter momento angular total diferente de zero.
O
momento angular total está para o movimento de rotação
assim como a quantidade de movimento total está para o movimento
de translação.
Como
p = mv, e usando expressão
 ,
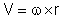podemos escrever o momento angular em termos de velocidade angular,
como
.
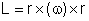Para
um sistema de partículas, definimos o momento angular total
como a soma dos momentos angulares de cada uma das partículas.
Para um sistema de N partículas, temos:
.
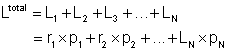Um
corpo em rotação tem um valor definido para o
momento angular. |
Pode-se,
portanto, dizer que, se o corpo está em rotação,
ele tem momento angular e vice-versa.
|
