Consideremos uma maçã sobre a qual marcamos uma pinta vermelha (r). Façamos agora a rotação da maçã em torno de seu eixo de simetria por um ângulo muito pequeno . A nova posição é agora . O deslocamento durante a rotação é dada por

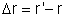
No caso de rotação de um ângulo em torno de um eixo podemos escrever a seguinte relação entre as coordenadas do vetor depois da rotação () e o vetor antes da rotação (r).

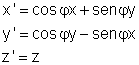
Para ângulos pequen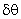os () temos:

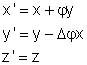
Portanto, o vetor deslocamento tem coordenadas

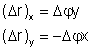
Vê-se pois que podemos escrever

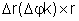
onde k é um versor, cuja direção e sentido angular são aqueles do eixo de rotação.

O vetor 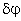k é o vetor deslocamento angular

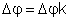
Esse vetor é deominado por .

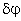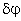= vetor deslocamento angular.

O vetor deslocamento angular pode agora ser escrito para angulas bem pequenos como:

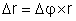
Observe que o vetor deslocamento angular é apenas uma generalização, para grandezas vetoriais, da relação entre espaço percorrido e ângulo, no caso do movimento circular. Lembramos que, naquele caso,
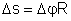