O momento angular de uma partícula é dado por

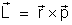
e a taxa de variação do momento angular em respeito ao tempo é

.

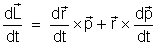O primeiro termo se anula uma vez que 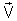é paralelo a 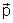. Utilizando a lei de Newton, escrevemos

.

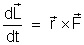O lado direito da equação acima é o torque da força definido como

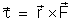
portanto, a taxa de variação do momento angular é igual ao torque aplicado pela força agindo sobre o corpo. Portanto

.

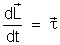Para um sistema de partículas, o momento angular total é dado por

.

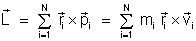No caso de uma distribuição contínua de partículas escrevemos para o momento angular

.

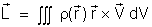Utilizando o sistema centro de massa verificamos que de ( ) e ( )

.

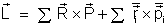e portanto, o momento angular do sistema pode ser expresso como o momento angular do centro de massa mais o momento angular de cada uma das partículas relativas ao centro de massa.