Em muitos casos é útil fazer uso de um sistema de coordenadas cuja origem coincide com o centro de massa do sistema. Assim a posição de uma partícula genérica do sistema (i-ésima partícula) é dada por

.

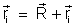Sua velocidade é composta por dois termos

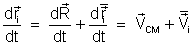
onde 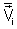representa a velocidade de partícula relativa ao sistema centro de massa. A aceleração é dada por

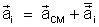
onde, novamente aqui, a barra representa a grandeza (no caso a velocidade) relativa ao centro de massa.

Multiplicando a equação ( ) por m_i, efetuando a soma e lembrando ( ) notamos uma propriedade da coordenada relativa ao centro de massa. Tal propriedade se resume, assim

.

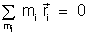Se considerarmos um sistema contínuo, então a propriedade análoga ( ) para um sistema contínuo é:

.

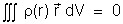Veremos que a propriedade ( ), ou equivalentemente ( ), é muito útil na simplificação da expressão de várias grandezas físicas quando expressas em termos do centro de massa.