|
Consideremos o caso mais simples de um sistema de partículas.
Aquele composto por apenas duas partículas. Nesse caso as equações
( ) se reduzem a apenas duas:
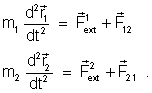
No
caso do sistema constituído por apenas duas partículas
definimos além do centro de massa
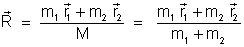
a
coordenada relativa
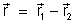
definimos,
além da massa total,
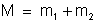
a massa reduzida
.
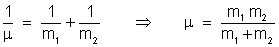A utilidade das grandezas físicas assim definidas podem ser
entendidas ao adicionarmos e subtrairmos as equações
( ). A adição nos leva a
.
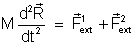Ao passo que a subtração nos leva, depois de dividirmos
a primeira equação por m1
e a segunda por m2, a
.
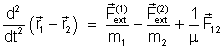A primeira equação representa o resultado já
conhecido de que o centro de massa se move de tal maneira que tudo
se passa como se todas as forças externas estivessem atuando
sobre ele.
Para entendermos a relevância da coordenada relativa e de massa
reduzida consideremos o caso em que o sistema de duas partículas
não está sujeito a forças externas. Nessas circunstâncias
as equações ( ) se escrevem agora
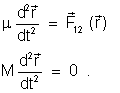
Uma vez conhecida a força (ou forças) de interação
entre as duas partículas podemos determinar a partir de ( )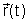
e utilizando ( ).
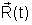Uma vez conhecidos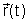
e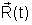
podemos determinar 
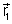e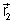 
utilizando ( ). Isto é
|
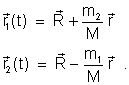
