| |

A geometria do espaço
tem como fundamento básico o conceito de distância.
Admitimos que o espaço é euclidiano, isto é,
nesse espaço são válidos os teoremas da geometria
euclidiana. Isto quer dizer que o comprimento de um intervalo é
dado por
 . .
Dizer que nesse espaço
valem os princípios da geometria euclidiana significa valer
regras tais como:
a) A soma dos ângulos
de um triângulo é igual a 180°.
b) Para um triângulo
retângulo vale o famoso teorema de Pitágoras
a2
= b2 + c2
onde a é a
hipotenusa e b e c são os demais lados do triângulo.
 |
A aplicabilidade da geometria euclidiana está intimamente
ligada a uma propriedade do espaço conhecida como curvatura.
|
Se a curvatura do espaço
for nula, sua geometria é euclidiana. Se a curvatura do espaço
for diferente de zero, o espaço é dito curvo. Nesse
caso, a geometria será dita riemanniana.

|
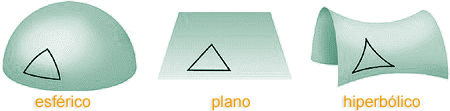
Para distinguirmos
uma geometria da outra, consideremos o caso de uma superfície
plana e uma superfície esférica. No caso do
plano, se tomarmos um ponto A e consideramos perpendiculares
por esse ponto até dois pontos B e C, verificaremos
que, para as distâncias a, b e c, vale o teorema de
Pitágoras
a2 = b2 + c2
ou
seja, o quadrado da hipotenusa é igual à soma
dos quadrados dos lados adjacentes. |
|
|
Consideremos
agora três pontos A, B, C sobre uma superfície
esférica. Seja um caso em que A e B estão sobre
a linha do Equador e C está sobre o Polo Norte. O caminho
mais curto que liga o ponto C sobre o Polo Norte até
um ponto sobre o Equador é, como sabemos, a linha de
longitude, a qual forma um ângulo reto com a linha do
Equador. Temos, pois, aqui um triângulo retângulo
tal que a = b.
Vemos pois que, sobre a esfera,
b2 + c2 > a2
|
|
Não vale, portanto,
o teorema de Pitágoras. Ademais, as somas dos ângulos
é maior que 180º.
As medidas de distância de objetos localizados no espaço
nos levarão, em geral, a decidir se o espaço é
curvo ou não. Nas medidas no cotidiano, e dentro das precisões
das medidas existentes, verificamos que a geometria do espaço
é euclidiana.
Einstein observou, no entanto, que a presença de massa afeta
a curvatura do espaço, isto significando que, rigorosamente,
a geometria euclidiana é válida apenas como uma aproximação,
aproximação essa muito boa para os fenômenos do
cotidiano que ocorrem na superfície terrestre.
Em regiões onde
o campo gravitacional é muito intenso (como nas proximidades
de um buraco negro), a curvatura do espaço deverá se
manifestar e, consequentemente, produzir efeitos físicos.

Gil Marques
|
|