No início do século XIX já havia a preocupação com a questão da validade da geometria de Euclides para o espaço tridimensional. O grande matemático alemão Carl Friedrich Gauss sugeria que para testá-la bastaria efetuar a soma dos ângulos internos de um triângulo. Gauss também percebera que, para haver desvios significativos o triângulo deveria ser suficientemente grande.

Utilizando-se de um teodolito, Gauss efetuou medidas de ângulos entre 3 cidades na Alemanha, entre os anos de 1821 e 1823. A maior distância entre elas era de aproximadamente 100 km. Os valores para os ângulos obtidos por Gauss foram:

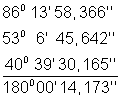
A verificação da aplicabilidade dos princípios da geometria euclidiana envolve portanto, medir ângulos de triângulos muito grandes. Poderíamos, por exemplo, tomar um triângulo, onde um dos vértices esteja sobre a Terra e os outros dois se localizem em estrelas ou galáxias distantes. No entanto, não podemos colocar teodolitos nas estrelas. Resta-nos assim fazer inferências através de outros métodos.

Existem duas evidências para o enrugamento do espaço. A primeira diz respeito ao encurvamento da luz pelo Sol. Isto se pode verificar experimentalmente durante uma eclipse do Sol. Os raios luminosos provenientes de uma estrela são ligeiramente curvados na direção do Sol quando eles passam pelas bordas do Sol. Tal efeito fora previsto por Einstein em 1917.

Outro efeito da rugosidade do espaço é a precessão da órbita de Mercúrio. Como Mercúrio é o planeta mais próximo do Sol, a trajetória de Mercúrio não é exatamente elíptica. Na realidade, sua órbita não é uma órbita fechada. Essa precessão da órbita é um efeito da curvatura do espaço.

De qualquer forma sabemos hoje que para escalas de distâncias relativamente grandes (da ordem de 10²⁵ m), a geometria de Euclides se aplica, o mesmo valendo para distâncias muito pequenas (cerca de 10^-15 m).

Gil Marques