Imaginemos dois pontos no espaço tridimensional tal que suas coordenadas (aqui utilizamos coordenadas generalizadas) sejam

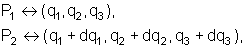
onde dq₁, dq₂, dq₃ são quantidades infinitesimais. Ou seja, os pontos estão muito próximos.

Definimos a ds distância entre dois pontos muito próximos (que diferem por quantidades infinitesimais dq_i das coordenadas generalizadas) por

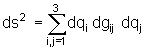
onde g_ij é o tensor métrico.

Se pudermos encontrar transformações

q₁ = q₁ (x, y, z),
q₂ = q₂ (x, y, z),
q₃ = q₃ (x, y, z) ,

tais que

ds_² = dx²+ dy² + dz²,

dizemos que o espaço é plano. De outra forma dizemos que o espaço é curvo.

Gil Marques