| |

Nesse capítulo
vamos abordar uma questão a respeito do espaço físico
que passou a ser relevante depois de trabalhos pioneiros de Einstein
ao propor a teoria geral da relatividade. Nessa teoria a matéria
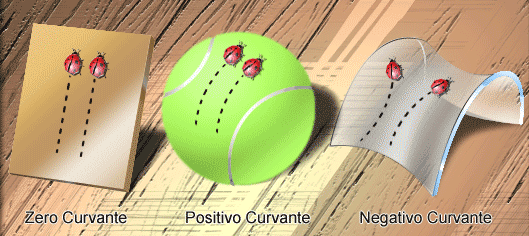
teria o efeito de curvar o espaço físico. Para entendermos
o que é um espaço curvo devemos começar definindo
o conceito de distâncias. Só podemos entender alguns
conceitos de geometria do espaço depois dessa definição.
Ou seja, a geometria do espaço tem como fundamento básico
o conceito de distância entre dois pontos.

Dado um espaço
euclidiano x, podemos definir uma função real d
- conhecida como distância - tal que, para os pontos a, b, c,x,
valem as propriedades:
| 1)
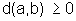
2) d(a,b) = d (b,a)
3)
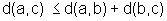
4)
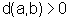
|
e |
d(a,a) = 0,
(simetria),
desigualdade triangular,
se
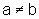 . .
|
Um espaço é
dito euclidiano se a distância entre dois pontos de coordenadas
| a = (a1,a2,a3) |
e |
b = (b1,b2,b3) |
é dada por
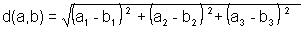
|
|