Em física, a maioria das grandezas envolvidas nas equações tem dimensão, isto é, são expressas em relação a uma unidade de medida. Isso faz com que a inclinação do gráfico que expressa um fenômeno físico tenha uma unidade e não possa ser interpretada como tangente de um ângulo, na maior parte dos casos.

Entretanto, sempre podemos definir a inclinação da reta a partir de um par qualquer de pontos (x₁,y₁) e (x₂,y₂), pela expressão

.

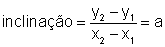Assim, o coeficiente a é uma grandeza com dimensão física quando as grandezas x e y não têm a mesma dimensão física. Por exemplo, se y mede posição em m e x mede tempo em s, a inclinação tem a dimensão de m/s.

É importante, ainda, ter atenção para o fato de que, apesar da reta que representa o gráfico y(x) formar um ângulo com o eixo Ox que pode ser medido, por exemplo, com um transferidor, não podemos dizer que o coeficiente a seja a tangente desse ângulo. Isso ocorre porque este ângulo depende da maneira como você escolhe as escalas. Por isso, para calcular a é necessário usar a expressão para a inclinação dada acima, embora seja comum chamá-lo de coeficiente angular.

Em relação ao coeficiente b, a interpretação é a mesma da situação anterior, exceto pelo fato dele possuir também uma dimensão física na maior parte dos casos.

Vito Vanin