| |
O número real a
é denominado coeficiente angular e está
associado à inclinação da reta em relação
ao eixo Ox. No caso (i) da prática
anterior, o coeficiente angular é igual a 2; no caso (ii)
é igual a 3. Note que a reta descrita pela função
do item (ii) é “mais inclinada” que a do item (i).
Se a for negativo (a < 0), como no item (iv), a grandeza y decresce
à medida que x cresce e a reta forma um ângulo maior
que 90o com o eixo x.
Podemos relacionar o coeficiente angular com o ângulo entre
a reta e o eixo Ox. Para relembrar porque, considere o triângulo
retângulo abaixo. Os dois lados que formam o ângulo reto
são chamados catetos. O lado q é o cateto oposto ao
ângulo
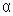 e o lado r é o cateto adjacente ao ângulo e o lado r é o cateto adjacente ao ângulo
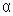 .
No triângulo retângulo define-se tangente de .
No triângulo retângulo define-se tangente de
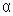 (abreviadamente tan (abreviadamente tan
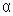 ) como a razão entre o cateto oposto a ) como a razão entre o cateto oposto a
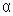 e o cateto adjacente:
e o cateto adjacente:
Assim, vemos que a constante a é igual
à tangente do ângulo que a reta forma com o eixo Ox.
Podemos definir as funções trigonométricas, como
seno, coseno e tangente, para qualquer ângulo. A tangente de
um ângulo 90º <
 < 180º tem sinal negativo e é igual em módulo
à tan (180º -
< 180º tem sinal negativo e é igual em módulo
à tan (180º -
 ). Com esta definição, o coeficiente a pode ser
interpretado como a tangente do ângulo que a reta y = ax + b
faz com o eixo x. Se a for negativo, o ângulo que a reta forma
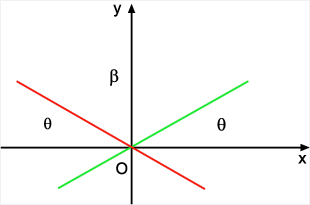
com o eixo x é obtuso e y diminui se x aumenta. A figura ao
lado mostra duas retas com coeficientes angulares de mesmo módulo
e sinais contrários. Chamando de a o coeficiente angular da
reta que forma ângulo ). Com esta definição, o coeficiente a pode ser
interpretado como a tangente do ângulo que a reta y = ax + b
faz com o eixo x. Se a for negativo, o ângulo que a reta forma
com o eixo x é obtuso e y diminui se x aumenta. A figura ao
lado mostra duas retas com coeficientes angulares de mesmo módulo
e sinais contrários. Chamando de a o coeficiente angular da
reta que forma ângulo
 com o eixo Ox, temos a > 0 e a reta que forma ângulo
com o eixo Ox, temos a > 0 e a reta que forma ângulo
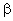 =180º -
=180º -
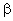 tem coeficiente angular -
tem coeficiente angular -
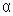 . .
O número real b corresponde ao valor
de y quando x = 0, ou seja, indica em que ponto a reta vai “cortar”
o eixo y. Note que a reta descrita pela função do item
(i) cruza o eixo Oy em y = 2 e a reta do item (iii) cruza o eixo y
em y = -1 . Como o coeficiente angular das duas retas é o mesmo
(a = 2), elas têm a mesma inclinação, ou seja,
são paralelas.

Vito Vanin
|
|