Estamos muito habituados a "fazer regra de três" em situações do cotidiano. Calculamos muito rapidamente que, se a dúzia de bananas custa R$2,40, uma dúzia e meia custará R$3,60. Dizemos que o preço da penca é proporcional ao número de bananas. Existem muitas outras situações onde há proporcionalidade entre grandezas, por exemplo, um mol de moléculas contém 6x10²³ moléculas.

Uma grandeza física que é uma proporção entre duas outras grandezas é a densidade dos corpos homogêneos - a densidade é a razão entre a massa e o volume do corpo. Dizer que o corpo é homogêneo significa dizer que as propriedades de qualquer fragmento são as mesmas do corpo todo.

Para fixar idéias nesta discussão, imagine uma usina de Alumínio. A densidade do Al é 2,7 g/cm³ = 2,7x103 kg/m³ . A fábrica produz, a partir de um grande corpo de Alumínio que podemos considerar puro nesta discussão, perfis, panelas e papel de Alumínio. Dizer que o grande corpo de Al é homogêneo, em relação à densidade, significa dizer que a proporção entre massa e volume é a mesma para qualquer pedaço desse corpo. Assim, tanto para um pedaço de papel de Alumínio quanto para um caco da panela ou um fragmento de um trilho de cortina, a razão entre massa e volume é r=2,7x103 kg/m³. Podemos, portanto, sempre deduzir o volume V de um objeto de Al como V=m/r. Quando o objeto tem Volume conhecido, podemos deduzir sua massa m como m=Vr.

O gráfico da figura abaixo representa essa propriedade do Alumínio metálico puro nas condições ambientes normais.

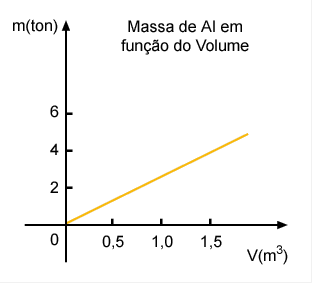
Note a propriedade, absolutamente importante, do gráfico da massa de Alumínio em função do volume passar pela origem do sistema de coordenadas, identificada pelo ponto O.

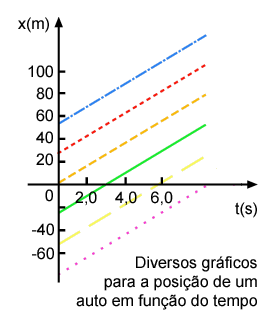
Quando lidamos com a velocidade de um objeto, tendemos a pensar que ela representa uma proporção. Afinal, dizer que um automóvel está correndo a 10 m/s significa que ele corre 10 m em 1 s. No entanto, a velocidade não é uma proporção entre a posição e o tempo. Veja, na figuras abaixo, diferentes possíveis gráficos da posição em função do tempo de um automóvel com velocidade v=10m/s.

Caso você, equivocadamente, imaginasse a velocidade como uma proporção entre posição e tempo, deduziria que a posição do automóvel em t=6,0s é x=60m. Vemos no gráfico acima que, exceto na situação descrita pela linha tracejada, a posição do automóvel em t=6,0s NÃO é x=60m.

Se a velocidade não é uma proporção, o que ela é? Resposta: é uma variação proporcional. Ela representa o deslocamento - uma variação de posição - num intervalo de tempo. Assim, a velocidade não é a proporção entre a posição e o tempo, mas sim a proporção entre variação de posição e "variação" de tempo. Quando um corpo mecânico desloca-se à velocidade constante, sua variação de posição é proporcional ao intervalo de tempo considerado, portanto, é uma variação proporcional.

Para pensar...

Nas situações mais simples onde há apenas um objeto em movimento uniforme, você pode escolher a origem do sistema de coordenadas de maneira que em t=0s ele esteja na origem. No entanto, isso não pode ser feito em geral, de maneira que NUNCA devemos pensar na velocidade como uma proporção entre posição e tempo, mesmo que isso dê certo em alguma situação muito particular.
Uma variação proporcional pode, com freqüência, ser expressa por números negativos, o que raramente faz sentido com proporções. Nas figuras abaixo mostramos alguns possíveis gráficos de posição em função do tempo para um objeto à velocidade de -5 m/s. A diferença entre as duas figuras é devida apenas ao intervalo de tempo considerado em cada um dos movimentos.

Descreva uma situação física de Movimento Uniforme onde você defina tempos negativos. Veja que basta escolher uma origem para a coordenada tempo posterior ao instante em que você começa a descrever a situação.

Vito Vanin