| |
Muitas vezes usaremos o valor do mensurando numa equação
para determinar uma outra grandeza qualquer. O que fazer com a incerteza
associada? Para o mensurando temos a incerteza
do processo de medida, enquanto que para grandezas determinadas
através de fórmulas temos a incerteza propagada.
O problema pode ser posto da seguinte maneira:
dada uma função w = w(x, y, z) onde x, y, z são
grandezas experimentais com incertezas dadas por
 x,
y,
z
e independentes entre si, quanto vale
w
? A independência entre
x,y,
zé
necessária para a validade das fórmulas a seguir, mas
não será discutida por enquanto.
Para simplificar suponha w apenas função de x. No gráfico
abaixo está representando w(x).
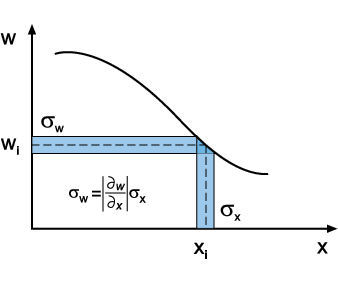
A incerteza de w, neste gráfico,
pode ser obtida pela simples projeção da incerteza de
x. Para pequenos intervalos no eixo x, temos em primeira ordem:
Para mais de uma variável independentes
entre si, podemos escrever uma fórmula geral (visualize uma
soma de catetos em n dimensões):
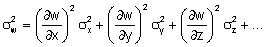
Acompanhe
os exemplos a seguir:
Considere
a soma de dois segmentos:
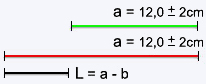
A incerteza no segmento soma pode ser calculada aplicando a equação
anterior:
que
resulta:
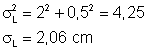
Logo
L = (20,0 ± 2,1) cm
Seguindo o mesmo esquema do exemplo anterior,
a incerteza associada à subtração de duas grandezas
experimentais é dada por:
Novamente,
usando a equação (2.3):
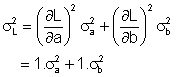
resulta:
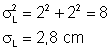
Logo
L
= (4,0 ± 2,8) cm
Note que na soma, tanto a grandeza como a
incerteza aumentaram, mas na diferença de duas grandezas experimentais,
apesar do resultado ser menor em módulo, a incerteza final
é maior que a das partes.
Vamos agora determinar o volume do cilindro
na figura abaixo em que se mediram o raio e a altura.
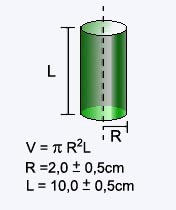
Propagaremos as incertezas em todos os termos do produto:
 ,
R e L.
Calculando cada um dos termos acima usando os valores fornecidso na
figura:
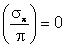(i)
(ii)
e
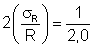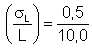(iii)
Somando
i, ii e iii em quadratura:
| MUITO IMPORTANTE: |
| Na equação acima, de propagação
de incertezas na multiplicação e divisão,
obtivemos a incerteza relativa
 .
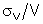NÃO ESQUEÇA DE MULTIPLICÁ-LA PELO RESULTADO
(V) PARA OBTER A INCERTEZA ABSOLUTA. Multiplicando V por V e ajustando o número de significativos...
|
O
resultado do volume do cilindor vale:
V = (126 ± 63) cm3
ou ainda
V = (13 ± 6) x 10 cm3
Os resultados acima são mais gerais
do que parece à primeira vista. Para as quatro operações
podem ser resumidos como segue:
Na soma ou subtração,
a incerteza absoluta do resultado é a soma em quadratura
das incertezas absolutas. |
| Na multiplicação ou
divisão, a incerteza relativa do resultado
é dada pela soma em quadratura das incertezas relativas
dos operandos (não esqueça de converter a incerteza
relativa em absoluta).
|
A seguir estão resumidos os principais
casos de propagação de incertezas. Uma importante regra
prática pode ser obtida se notarmos que o resultado de propagação
de incertezas não precisa ser feito com precisão numérica
maior que cerca de 5%. Logo:
Qualquer termo menor que 1/3 do maior
termo na soma em quadratura pouco contribui no resultado final e em
geral, pode ser desprezado.
| Exemplificando: |
|
Volte para o exemplo :
Lá calculamos o resultado de:
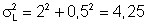
observe que 0,52 << 22,
ou seja, se desprezarmos o termo menor, o resultado seria
4,00, que arredondado para um significativo resultaria sL=
2 cm, não muito diferente do resultado anterior, 2,1
cm.
Algebricamente: sejam x1
e x2 os termos de uma soma
em quadratura com x2 = k
x1. A soma em quadratura
resulta:
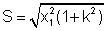
Seja agora
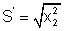
em que
se desprezou x1 uma vez que k>1. Note que S
> S', uma vez que x2> x1. Queremos
saber, o menor valor de k de forma que S' e S não difiram
em mais que 5%. Queremos que
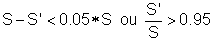
Com alguma
manipulação algébrica se obtém
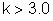
Isto pode simplificar muito as contas pois,
numa soma em quadratura, podemos simplesmente desprezar termos
menores que 1/3 do maior. Isto permite, na maioria das vezes,
um cálculo rápido, sem o uso de calculadora.
Atente que são os termos da soma em quadratura
que devem ser comparados, não as incertezas.
|
Manfredo
H. Tabacniks
|
|
