| |

Um processo de medida tem sempre por objetivo
determinar o valor médio verdadeiro, ymv
, de uma grandeza, cujo valor verdadeiro é yv.
Acontece que, em geral, o valor verdadeiro nos é desconhecido,
e para se obter o valor médio verdadeiro, são necessárias
infinitas medidas!
Dessa forma, para um conjunto de medidas,
{y1, y2, y3, ...yn},
o valor médio verdadeiro é dado por:

Como em geral ymv é um valor inacessível, usam-se estimativas:
a média dada pela equação
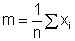 ,
,
a estimativa do desvio padrão
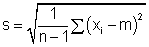
e do desvio padrão da média
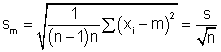 . .
Apenas relembrando alguns termos novos que
usaremos com frequência:
MENSURANDO: Grandeza a ser
determinada num processo de medição.
VALOR VERDADEIRO: Valor
consistente com a definição de uma determinada quantidade.
Em princípio, apenas obtido num processo de medida perfeito.
INCERTEZA: Parâmetro
associado ao resultado de uma medida que caracteriza a dispersão
dos valores que podem satisfato-riamente ser atribuidos ao mensurando.
Reflete o desconhecimento do valor exato do mensurando.
ERRO: É a diferença
entre a medida e o valor verdadeiro. Quanto menor o erro maior a exatidão
(acurácia).
ERRO SISTEMÁTICO:
Erro constante característico do processo ou instrumento.
ERRO PADRÃO: Desvio
padrão dos valores médios em relação ao
valor verdadeiro.
A grande diferença entre a incerteza
e o erro (seja ele qual for) é que o erro pode, em princípio,
ser ‘corrigido’ enquanto a incerteza é um intervalo
de confiança das medidas. Logo, caso sua experiência
tenha um erro, existe uma falha no procedimento que pode e deve ser
corrigido.

Medida da tensão de uma pilha.
Neste exemplo, pretendemos determinar o valor
mais provável e a respectiva incerteza da tensão
de uma pilha. Usaremos um voltímetro cuja incerteza
nominal (fornecida pelo fabricante) é de 1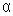 = 0,25% do valor indicado.
= 0,25% do valor indicado. |
 |
A incerteza do processo de medida deve, portanto, ser combinada
com a incerteza do fabricante, para gerar o resultado procurado.
Algumas fórmulas utilizadas serão explicadas adiante.
Retorne ao exemplo assim que terminar a leitura deste capítulo.
As medidas realizadas estão na tabela a seguir.
| n |
U (volt) |
incerteza nominal (V) |
| 1 |
1,572 |
0,004 |
| 2 |
1,568 |
0,004 |
| 3 |
1,586 |
0,004 |
| 4 |
1,573 |
0,004 |
| 5 |
1,578 |
0,004 |
| 6 |
1,581 |
0,004 |
Tabela 1 - Tensão de uma pilha medida
com voltímetro (incerteza nominal 0,25%)
Antes, um comentário: a tabela 1 acima
tem três colunas. A última contém a incerteza
nominal das medidas que, como vemos, não varia ao longo das
medidas. A tabela poderia ter apenas 2 colunas e a incerteza das medidas
ser incorporada no título da coluna 2. A nova tabela ficaria
como no exemplo abaixo:
| n |
U ± 0,004 (V) |
| 1 |
1,572 |
| 2 |
1,568 |
| 3 |
1,586 |
| 4 |
1,573 |
| 5 |
1,578 |
| 6 |
1,581 |
Tabela 2 - Tensão de uma pilha medida
com voltímetro (incerteza nominal 0,25%)
Vamos aos cálculos. Note que em cálculos
intermediários usamos um dígito significativo a mais,
para apenas no final expressarmos o valor da medição
conforme as normas discutidas no capítulo anterior.
Valor médio:
 V V
Desvio padrão das medidas:

Desvio padrão do valor médio:
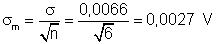
Incerteza nominal do voltímetro
(0,25% da medida):
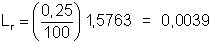 V V
Verifique que o desvio padrão das
medidas (na realidade do processo de medição)
é maior que a incerteza nominal do voltímetro. Isso
era esperado, pois, na composição da incerteza do processo
de medidas, a incerteza do voltímetro é apenas um dos
componentes. Uma única medida, por exemplo, a primeira medida
na Tabela 2, pode ser expressa como:
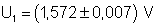
A incerteza de nossa medida difere da incerteza
nominal citada na tabela 1. Tivemos que fazer uma série de
medidas para determinar o NOSSO desvio padrão.
Uma vez que realizamos uma série de
6 medidas, podemos expressar nosso resultado de forma mais precisa,
usando o valor médio das seis medidas e seu desvio padrão
(o desvio padrão da média). Portanto nosso resultado
ficaria assim:
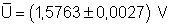
Este resultado está ótimo para
desenvolver nossos estudos e verificar alguma dependência da
tensão da pilha com outras grandezas. Mas o nosso voltímetro
pode ter um erro de calibração. Explicando:
Na fábrica são produzidos milhares de voltímetros.
Em média todos iguais. Mas no varejo, ao comparar os valores
medidos por diferentes voltímetros, um indica um valor um pouco
maior, outro um pouco menor... Como então comparar medidas
feitas com voltímetros diferentes? Temos que
retornar ao manual do aparelho e procurar a incerteza de calibração
do mesmo, ou seja, o desvio padrão de calibração
dos voltímetros. Em geral (mas não necessariamente)
a incerteza do instrumento e o desvio padrão de calibração
são semelhantes. Seria um desperdício se assim não
fosse.
 |
(Quem compraria um aparelho muito preciso
e caro mal calibrado? Por que calibrar cuidadosamente um
aparelho vagabundo?). Podemos supor então que o desvio
padrão de calibração do voltímetro
é da mesma ordem que sua incerteza nominal. |
 |
Dessa forma é
possível que instrumentos diferentes indiquem valores diferentes
para uma mesma medida, nesse nosso caso, com um desvio padrão
de 0,004V. Caso tenhamos em nosso laboratório mais que um voltímetro
do mesmo modelo, temos que incorporar esse “desvio padrão
de calibração” em nosso resultado. Isso pode ser
feito por meio de uma soma quadrática, denominada de erro padrão,
em que se compõe quadraticamente o desvio padrão da
média com o desvio padrão de calibração
do instrumento:
Erro padrão:
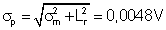
Finalizando, o valor mais provável
da tensão da pilha pode ser representado por:
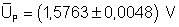
Afinal, qual o valor que devemos usar? Depende.
Para comparar séries de medidas no mesmo instrumento, podemos
usar a média
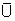 e o desvio padrão da média.
e o desvio padrão da média.
Para comparar medidas entre si,
basta o desvio padrão.
Para comparar medidas em instrumentos
diferentes, precisamos do erro padrão.
Manfredo H. Tabacniks
|
|