Quando se trabalham com vários resultados em condições de repetitividade de uma medição, usam-se algumas estatísticas para resumir e consolidar as informações obtidas. Por exemplo: ao tentar determinar o tempo de queda de um corpo, um aluno mediu uma única vez o evento. Tendo a incerteza do aparelho utilizado, poderíamos ter uma idéia do acerto do aluno. Mas a incerteza cobre apenas o erro do aparelho e não a do aluno ou mesmo do procedimento experimental.
O problema que se coloca é:

COMO DETERMINAR A INCERTEZA DE UMA MEDIDA?

Uma abordagem alternativa para este problema é medir várias vezes o mesmo tempo e calcular a média. A variabilidade de cada medida é dada pelo desvio padrão e a variabilidade da média (caso se obtenham várias médias) será dada pelo desvio padrão da média.

O problema é que para o valor mais provável a partir de médias, determinar desvios padrão e desvio padrão de médias exige que se façam INFINITAS medidas e definitivamente não temos tempo para isso! Vamos, portanto, ESTIMAR o valor mais provável, o desvio padrão e o desvio padrão da média para um conjunto pequeno de medidas. O desenvolvimeto teórico e a justificativa para esse procedimento podem ser encontrados em qualquer livro texto básico de estatística, como, por exemplo, Helene e Vanin (1981).

A média, o desvio padrão e o desvio padrão da média, para um conjunto finito com n dados podem ser estimados aplicando as equações abaixo.

média de uma amostra com n valores:

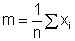
desvio padrão de uma amostra:

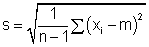
desvio padrão da média com n valores:

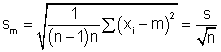
Manfredo H. Tabacniks