|
Vimos
que o trabalho é uma medida da variação da energia cinética, isto
é,
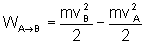
Portanto, se considerarmos as duas expressões sobre o trabalho realizado
entre A e B, podemos escrever para forças conservativas as identidades
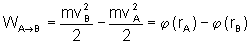
ou
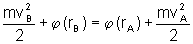
À
soma da energia potencial e da energia cinética damos o nome de Energia
Mecânica.
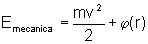
Como na expressão acima os pontos A e B são arbitrários, concluímos
que ele vale para qualquer ponto. Donde concluímos:
| A
energia mecânica é conservada |
Naturalmente,
o resultado acima só faz sentido para forças conservativas.
Agora entendemos melhor o que significa uma força ser conservativa.
Para essas forças, quando nos deslocamos de um ponto para outro, a
energia mecânica se conserva. Isto é, assume o mesmo valor em qualquer
ponto do espaço.

Marques e Ueta
|