|
Pode-se
também relacionar trabalho realizado por uma força com energia potencial.
Tendo em vista a existência de duas categorias de forças, podemos
nos perguntar sobre a forma de distingui-las. Novamente aqui utilizamos
o conceito de trabalho.
Consideremos o deslocamento de uma partícula de um ponto A para um
ponto B do espaço.
Existem
infinitas maneiras de irmos de um ponto A até o ponto B. Podemos utilizar
infinitos caminhos (ou seja, trajetórias), por exemplo, pelos caminhos
1, 2 ou 3 da figura. Dizemos que uma força é conservativa se o trabalho
realizado pela força não depender do caminho utilizado para irmos
de A até B.
Outra definição equivalente a essa é dizer que uma força é conservativa
quando, para um caminho fechado qualquer (isto é, indo de A até A),
o trabalho é nulo.
Já vimos que uma força é conservativa se o trabalho realizado no percurso
de A até B só depende dos pontos A e B. Como os pontos A e B têm posição
rA e rB,
escrevemos matematicamente:
onde
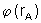é uma função de rA (isto é, depende
de rA) e é a energia potencial em
A, e
é a mesma função calculada B (de coordenada rB)
e é a energia potencial em B.
Note-se
que essa condição leva naturalmente a
O
fato de que
deve se anular explica a razão para o sinal "menos" na equação
.
A função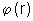 
é a função Energia Potencial.
Marques e Ueta
|
