Há três tipos de associação de geradores:

a) em série              
b) em paralelo, ou em derivação              
c) mista.

É aquela em que se liga o polo positivo de um gerador ao polo negativo do seguinte.

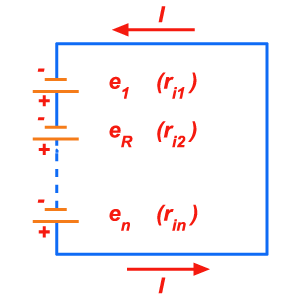
O circuito externo é ligado ao polo positivo do primeiro e ao polo negativo do último.  As características dessa associação são as seguintes.

Na associação em série, em qualquer parte do circuito a corrente tem a mesma intensidade.  Se introduzirmos novos geradores, a intensidade aumenta; se retirarmos, a intensidade diminui.  Mas para o mesmo número de geradores, ela tem o mesmo valor em qualquer parte do circuito.

Sejam 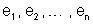   as forças eletromotrizes dos geradores; 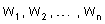, as energias fornecidas pelos geradores, durante um tempo t.  Temos, de acordo com :

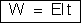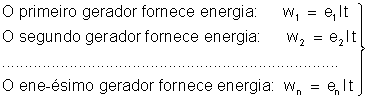                    (1)

A energia fornecida pela associação é igual à soma das energias que os geradores fornecem.  Seja W essa energia total.  Teremos:

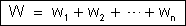                                     (2)

Suponhamos um gerador equivalente à associação, isto é, um gerador que fornece a mesma corrente I, e, durante o tempo t fornece a mesma energia W que a associação fornece.  Para isso, esse gerador deve ter uma f.e.m. que chamaremos E que ainda não conhecemos, mas que deve satisfazer à equação: 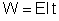.  Comparando com as relações (1) e (2), temos:

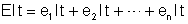
ou

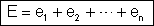
Concluímos que na associação em série a força eletromotriz total, que é a f.e.m. do gerador equivalente, é a soma das forças eletromotrizes.

Sejam 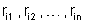 , as resistências internas dos geradores.  Como eles estão em série , a resistência total é igual a soma das resistências dos geradores.

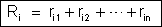
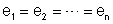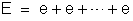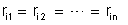
Os geradores são iguais.  Temos:  1o – As f.e.m. são iguais, isto é, .  Chamando e à essa f.e.m. igual, resulta para a f.e.m. da associaçao:  (n parcelas)       ou        2o – As resistências internas são iguais, isto é, Chamando 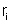 à essa resistência interna igual para todos, resulta, para a associação:

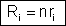
Estudaremos a associação em paralelo só para o caso em que os geradores são iguais.  Nessas associações, os polos positivos são ligados entre si e constituem o polo positivo da associação (ponto P); os polos negativos são ligados entre si e constituem o polo negativo da associação (ponto N).  Seja i a intensidade fornecida por um gerador, e a força eletromotriz de cada gerador e w a energia fornecida por cada gerador, durante o tempo t.

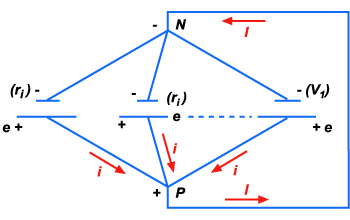
As correntes i reunem-se no ponto P e dão a corrente fornecida pela associação.  Pela primeira lei de Kirchhoff temos:

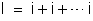   (n parcelas)

ou

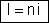
A energia fornecida por um gerador é: 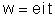  (1).

Sendo W a energia fornecida pela associação, temos:

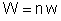
Chamamos gerador equivalente à associação a um gerador que fornece para o circuito externo a corrente I, e, durante o tempo t fornece a mesma energia W que a associação fornece.  Para isso ele deve ter uma f.e.m. E, que não conhecemos ainda, mas que deve satisfazer à equação:

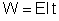. Sendo  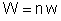, temos:

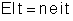 .Mas 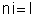 . Então

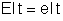 , ou

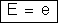
Concluímos que numa associação em paralelo a força eletromotriz da associação é igual à força eletromotriz de cada gerador, quando os geradores são iguais.

Os geradores têm a disposição de condutores associados em paralelo.  Sendo 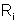 a resistência interna da associação, temos:

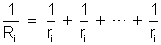    (n parcelas)

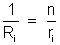          ou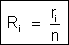          

A resistência total da associação é 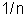  da resistência de cada gerador.

É aquela em que diversas associações em série são ligadas em paralelo, ou vice-versa. Deduzamos as fórmulas tomando por base a primeira figura abaixo:

Seja:

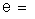f.e.m. de um gerador
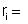resistência interna de um gerador
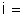corrente fornecida por um gerador
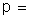número de geradores em cada associação em paralelo
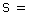número de associações em paralelo ligadas em série (na segunda figura acima, s é o número de geradores de cada série e p o número de séries ligadas em paralelo).

Tomemos como base a primeira figura acima.  Cada associação em paralelo tem as características seguintes:

1 – f.e.m.: de acordo com 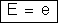, a f.e.m. de cada uma é igual a e.

2 – intensidade de corrente: de acordo com 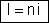cada asociação fornece corrente igual a pi.

3 – resistência interna: de acordo com 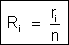vale .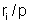

A associação final terá, de acordo com as fórmulas 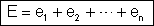, 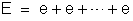e com o que vimos sobre a corrente a respeito da associação em série:

1  –  f.e.m.:  
2  –  resistência interna:  
3  –  corrente: